Összetett logaritmus - Complex logarithm

A komplex logaritmus egyetlen ága. A színárnyalat a színt használják, hogy bemutassák a arg (poláris koordináta szöge) a komplex logaritmus. A szín telítettségét és értékét (intenzitása és fényessége) használják a komplex logaritmus modulusának megjelenítésére .

A matematikában a komplex logaritmus a természetes logaritmus általánosítása nem nulla komplex számokra . A kifejezés az alábbiak egyikére utal, amelyek szorosan kapcsolódnak egymáshoz:

Egy nem zérus $z$ komplex szám komplex logaritmusa , amelyet bármilyen $w$ komplex számnak definiálunk, amelyre $e w = z$ . Az ilyen $w$ számot $log z$ jelöli . Ha $Z$ van megadva poláris formájú , mint $a Z = újra iθ$ , ahol $R$ és $θ$ valós számok a $r > 0$ , akkor $ln (r) + iθ$ egyike logaritmusa $z$ , és az összes komplex logaritmusai $z$ pontosan a számok a formájában $ln (r) + i (θ + 2 π k)$ számára egészek k . Ezek a logaritmusok egyenlő távolságra vannak a komplex sík függőleges vonala mentén.
Komplex értékű függvény , amely a nullától eltérő komplex számok halmazának valamely részhalmazán van definiálva , és mindenki számára kielégítő . Az ilyen komplex logaritmusfüggvények analógok a valódi logaritmusfüggvénnyel , amely a valós exponenciális függvény fordítottja , és így kielégíti az $e$ $ln$ $x$ $=$ $x$ értéket minden pozitív $x$ valós szám $esetén$ . A komplex logaritmusfüggvények valós értékű függvényeket tartalmazó explicit képletekkel, az integrációval vagy az analitikus folytatás folyamatával hozhatók létre . ${\ displaystyle \ log \ kettőspont U \ \ \ mathbb {C}}$ ${\ displaystyle U}$ ${\ displaystyle \ mathbb {C} ^{*}}$ ${\ displaystyle e^{\ log z} = z}$ ${\ displaystyle z}$ ${\ displaystyle U}$ ${\ displaystyle \ ln \ colon \ mathbb {R} _ {> 0} \ to \ mathbb {R}}$ ${\ displaystyle 1/z}$

Nincs definiált folyamatos komplex logaritmus függvény . Kezelésének módjai ez tartalmazza ágak , a hozzá tartozó Riemann-felület és a részleges inverzeit a komplex exponenciális függvény . A legfőbb értéke határozza meg egy adott komplex logaritmus függvény , amely folytonos, kivéve mentén negatív valós tengelyen; a komplex síkon a negatív valós számok és a 0 eltávolítása esetén a (valódi) természetes logaritmus analitikus folytatása . ${\ displaystyle \ mathbb {C} ^{*}}$ ${\ displaystyle \ operatornév {Log} \ kettőspont \ mathbb {C} ^{*} \ to \ mathbb {C}}$

Problémák a komplex exponenciális függvény megfordításával

A komplex logaritmusfüggvény többértékű képzeletbeli részének ábrája, amely az ágakat mutatja. Ahogy egy z komplex szám megkerüli az origót, a logaritmus képzeletbeli része felfelé vagy lefelé megy. Ez teszi az origót a függvény elágazási pontjává .

Ahhoz, hogy egy függvénynek inverze legyen, külön értékeket kell leképeznie különböző értékekre ; vagyis injektívnek kell lennie . De a komplex exponenciális függvény nem injektıv, mert e ^{w +2 kπi} = e ^w bármely komplex szám w és egész k , mivel hozzátéve iθ hogy W az a hatása, forgó e ^w az óramutató járásával ellentétes θ radián . Tehát a pontok

{\ displaystyle \ ldots, \; w-4 \ pi i, \; w-2 \ pi i, \; w, \; w+2 \ pi i, \; w+4 \ pi i, \; \ ldots ,}

függőleges vonal mentén egyenlő távolságra elhelyezve, az exponenciális függvény mindegyike azonos számra van leképezve. Ez azt jelenti, hogy az exponenciális függvénynek nincs standard értelemben fordított függvénye. Erre a problémára két megoldás létezik.

Az egyik az, hogy az exponenciális függvény tartományát olyan régióra korlátozzuk, amely nem tartalmaz két számot, amelyek 2πi egész többszörösével különböznek : ez természetesen a log z ágainak meghatározásához vezet , amelyek bizonyos függvények, amelyek egy logaritmust különítenek el minden szám a saját tartományában. Ez analóg a meghatározása arcsin x a [-1, 1] , mint az inverze a korlátozása sin θ az intervallum [- π / 2, π / 2] : végtelen sok valós számok θ a sin θ = x , de az ember önkényesen választja ki a [ - π /2, π /2] -ben lévőt .

A határozatlanság feloldásának másik módja az, hogy a logaritmust olyan függvénynek tekintjük, amelynek tartománya nem egy régió a komplex síkban , hanem egy Riemann-felület, amely végtelenül 1-ig lefedi a lyukas komplex síkot.

Az ágak előnye, hogy komplex számokkal értékelhetők. Másrészt a Riemann -felület funkciója elegáns, mivel a logaritmus minden ágát összecsomagolja, és nem igényel önkényes választást a meghatározás részeként.

Fő érték

Meghatározás

Minden egyes nemnulla komplex szám Z , a legfőbb érték Log Z a logaritmusa, amelynek képzetes rész rejlik az intervallum (- π , π ]. Az expressziós Log 0 nem határozza, mivel nincs komplex szám w kielégíti e ^w = 0.

Komplex számok esetében, amelyek nem nem pozitív valós számok, a komplex logaritmus fő értéke a természetes logaritmus analitikus folytatása . Negatív komplex számok esetén a főértéket úgy kapjuk meg, hogy tovább folytatjuk, ha negatív valós számokat fejezünk ki, mint komplex számok pozitív imgináris részeit.

Ha a z jelölési napló úgy jelenik meg, hogy nincs megadva külön logaritmus, általában a legjobb azt feltételezni, hogy a főértéket szándékozzák. Ez különösen az ln z valós értékével összhangban álló értéket ad, ha z pozitív valós szám. A feliratozási napló nagybetűit néhány szerző arra használja, hogy megkülönböztesse a főértéket a z más logaritmusaitól .

A főérték kiszámítása

A poláris formájú egy nemnulla komplex szám $Z = x + yi$ jelentése $Z = újra iθ$ , ahol a abszolút értéke a $Z$ , és $θ$ van annak érv . Az abszolút érték valós és pozitív. Az érvelés meghatározott akár hozzáadásával egész szám többszöröse $2$ $π$ . Fő értéke a $( -$ $π$ $,$ $π$ $]$ intervallumhoz tartozó érték , amelyet $atan2 ($ $y$ $,$ $x$ $) formában$ fejezünk ki . ${\ texttyle r = | z | = {\ sqrt {x^{2}+y^{2}}}}$

Ez a következő képlethez vezet a komplex logaritmus főértékéhez:

{\ displaystyle \ operatornév {Napló} z = \ ln r+i \ theta = \ ln | z |+i \ operatornév {Arg} z = \ ln {\ sqrt {x^{2}+y^{2}} }+i \ operatornév {atan2} (y, x).}

Például $Log (-3 i) = ln 3 - πi /2$ , és $Log (-3) = ln 3 + πi$ .

A fő érték fordított függvényként

A Log z leírásának másik módja a komplex exponenciális függvény korlátozásának inverze, mint az előző részben. Az S vízszintes sáv, amely w = x + yi komplex számokból áll, úgy, hogy - π < y ≤ π egy példa egy olyan régióra, amely nem tartalmaz két számot, amelyek 2 πi egész többszörösével különböznek , így az exponenciális függvény S -re való korlátozása fordítottja van. Valójában az exponenciális függvény S -t bijektíven leképezi a defektes komplex síkra , és ennek a korlátozásnak a fordítottja az . Az alábbi konformális leképezési szakasz részletesebben ismerteti ennek a térképnek a geometriai tulajdonságait. ${\ displaystyle \ mathbb {C} ^{*} = \ mathbb {C} \ setminus \ {0 \}}$ ${\ displaystyle \ operatornév {Log} \ kettőspont \ mathbb {C} ^{*} \ S}$

Tulajdonságok

Nem minden, az ln által kielégített azonosság terjed ki a komplex számokra. Igaz, hogy e ^{Log z} = z minden z ≠ 0 (ez mit jelent az Log z lenni logaritmusa z ), de a személyazonosság Log e ^z = z meghiúsul z sávon kívül eső S . Emiatt nem mindig lehet a naplót alkalmazni az identitás mindkét oldalára e ^z = e ^w z = w levezetésére . Ezenkívül az azonossági napló ( z ₁z ₂ ) = Log z ₁ + Log z ₂ meghiúsulhat: a két oldal 2 πi egész többszörösével térhet el ; például,

{\ displaystyle \ operatornév {Log} ((-1) i) = \ operatorname {Log} (-i) = \ ln (1)-{\ frac {\ pi i} {2}} =-{\ frac { \ pi i} {2}},}

de

{\ displaystyle \ operatornév {Log} (-1)+\ operatorname {Log} (i) = \ left (\ ln (1)+\ pi i \ right)+\ left (\ ln (1)+{\ frac {\ pi i} {2}} \ right) = {\ frac {3 \ pi i} {2}} \ neq -{\ frac {\ pi i} {2}}.}

A Log z függvény minden negatív valós számnál szakaszos, de mindenhol máshol folyamatos . A diszkontinuitás magyarázataként fontolja meg, hogy mi történik Arg z -vel, amikor z megközelíti a negatív valós számot a . Ha Z közelít egy felülről, majd Arg z megközelíti π , amely szintén a értéke Arg egy önmagában. De ha Z közelít egy alulról, majd Arg z megközelítések - π . Tehát Arg z 2 π -vel "ugrik", mivel z keresztezi a negatív valós tengelyt, és hasonlóan Log z ugrik 2 πi -vel . ${\ displaystyle \ mathbb {C} ^{*}}$

A komplex logaritmus ágai

Van egy másik módja annak, hogy válasszon egy logaritmus minden nemnulla komplex szám úgy, hogy egy függvény L ( z ), amely folytonos minden az ? A válasz nem. Hogy megértsük, miért, képzeljük el, hogy egy ilyen logaritmusfüggvényt az egységkör mentén nyomon ^{követünk úgy} , hogy az L ( e ^iθ ) ^{értékét úgy értékeljük ki} , hogy θ 0 -ról 2 π -re nő . Ha L ( z ) folytonos, akkor L ( e ^iθ ) - iθ is , de ez utóbbi e ^iθ két logaritmusának különbsége , tehát értékeket vesz fel a diszkrét halmazban , tehát állandó. Különösen L ( e ²^πi ) - 2 πi = L ( e ⁰ ) - 0, ami ellentmond L ( e ²^πi ) = L (1) = L ( e ⁰ ). ${\ displaystyle \ mathbb {C} ^{*}}$ ${\ displaystyle 2 \ pi i \ mathbb {Z}}$

A komplex számokon meghatározott folyamatos logaritmus megszerzéséhez ezért szükséges a tartományt a komplex sík kisebb U részhalmazára korlátozni . Mivel az egyik cél a függvény megkülönböztetése , ésszerű feltételezni, hogy a függvény a tartomány minden pontjának szomszédságában van definiálva; más szóval, U legyen nyílt halmaz . Azt is, hogy ésszerű feltételezni, hogy U van kötve , mert különben a függvény értéke a különböző komponensek U lehet független egymástól. Mindez motiválja a következő meghatározást:

Egy ág log Z egy folytonos függvény L ( Z ) meghatározott egy csatlakoztatott nyitott részhalmaza U a komplex síkban úgy, hogy az L ( Z ) egy logaritmusa z minden egyes z a U .

Például a főérték definiál egy ágat a nyílt halmazon, ahol folytonos, ami az a halmaz , amelyet a 0 és az összes negatív valós szám eltávolításával kapunk a komplex síkból. ${\ displaystyle \ mathbb {C} -\ mathbb {R} _ {\ leq 0}}$

Egy másik példa: A Mercator sorozat

{\ displaystyle \ ln (1+u) = \ összeg _ {n = 1}^{\ infty} {\ frac {(-1)^{n+1}} {n}} u^{n} = u -{\ frac {u^{2}} {2}}+{\ frac {u^{3}} {3}}-\ cdots}

lokálisan egyenletesen konvergál a | u | <1, tehát a z = 1+ u beállítás a napló z ágát határozza meg az 1 sugarú nyitott lemezen, amelynek középpontja 1. (Valójában ez csak a Log z korlátozása , amint azt a különbség megkülönböztetése és az értékek összehasonlítása is mutatja 1. -kor.)

Ha egy ág rögzítve van, akkor azt "log z " -nek lehet jelölni, ha nem okozhat zavart. A különböző ágak azonban különböző értékeket adhatnak egy adott komplex szám logaritmusához, ezért egy ágat előre rögzíteni kell (különben a főágat kell érteni), hogy a "log z " pontos és egyértelmű jelentést kapjon.

Ágvágások

A fenti érvelés magában foglaló egység kör általánosítható azt mutatják, hogy nem ága log z létezik nyílt halmaz U tartalmazó zárt görbe , amely szél körül 0. Az egyik azt mondja, hogy „log z van egy elágazási pont , 0”. Annak elkerülése érdekében, hogy a 0 köré kanyarodó zárt görbéket ne tartalmazzuk, az U -t jellemzően a 0 -tól (beleértve) a végtelenig terjedő sugár vagy görbe kiegészítéseként választjuk. Ebben az esetben, a görbe néven ismert ág vágott . Például a fő ág egy ágát vágja a negatív valós tengely mentén.

Ha az L ( z ) függvényt az ágvágás egy pontján meg kell határozni, akkor szükségszerűen megszakítás nélküli lesz; legjobb esetben is folyamatos lesz "az egyik oldalon", mint a Log z negatív valós számnál.

A komplex logaritmus deriváltja

Minden ág $L (Z)$ a $log Z$ nyílt beállított $U$ inverze korlátozásának az exponenciális függvény, azaz a korlátozás a kép $L (U)$ . Mivel az exponenciális függvény holomorf (azaz komplexen differenciálható) nem romló deriváltal, az inverz függvény tételének komplex analógja érvényes. Ez azt mutatja, hogy $az L (Z)$ van Holomorf a $U$ , és $L'(Z) = 1 / z$ minden egyes $z$ a $U$ . Ennek bizonyítására egy másik módszer a Cauchy – Riemann -egyenletek ellenőrzése a poláris koordinátákban .

Ágak építése integrációval

A valós függvény a képlet segítségével állítható össze ${\ displaystyle \ ln (x)}$ ${\ displaystyle x> 0}$

{\ displaystyle \ ln (x) = \ int _ {1}^{x} {\ frac {du} {u}}.}

Ha a tartomány integrációs kezdődött pozitív szám egy 1-től eltérő, a képlet kellene

{\ displaystyle \ ln (x) = \ ln (a)+\ int _ {a}^{x} {\ frac {du} {u}}}

helyette.

A komplex logaritmus analógjának kidolgozásakor további bonyodalmak merülnek fel: a komplex integrál meghatározása útvonalválasztást igényel. Szerencsére, ha az integrandus Holomorf, akkor az az integrál értékét változatlan által deformálásával path (miközben a végpontok rögzített), és egy egyszerűen csatlakoztatva régió U (régióból „nincs lyuk”), minden olyan utat egy a Z belső U lehet folyamatosan deformálódik belsejében U bármely más. Mindez a következőkhez vezet:

Ha U egy egyszerűen csatlakoztatva nyitott részhalmaza nem tartalmazó 0, akkor egy ága log Z definiált U lehet kialakítani választásával kiindulási pont egy a U , kiválasztják a logaritmusa b az egy , és meghatározó

{\ displaystyle \ mathbb {C}}

{\ displaystyle L (z) = b+\ int _ {a}^{z} {\ frac {dw} {w}}}

az egyes Z a U .

A komplex logaritmus, mint konformális térkép

A Re (Log z ) = körök állandóak és az Im (Log z ) = konstansak a komplex z -síkban.

Bármilyen Holomorf térképet kielégítő az összes egy konform térkép , amely azt jelenti, hogy ha a két görbe ponton átmenő egy az U szöget zárnak α (abban az értelemben, hogy az érintők , hogy a görbék egy szöget zárnak α ), akkor a képek a két görbe képezik ugyanazon szög α at f ( a ). Mivel a log z egyik ága holomorf, és mivel az 1/ z származéka soha nem 0, ezért konformális térképet határoz meg. ${\ displaystyle f \ kettőspont U \ \ \ mathbb {C}}$ ${\ displaystyle f '(z) \ neq 0}$ ${\ displaystyle z \ in U}$

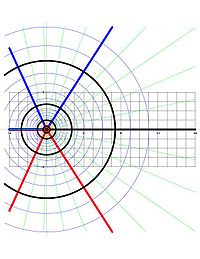
Például a w főágaság = Log z , leképezésként tekintve az | Im z | által meghatározott vízszintes csíkra < π , a következő tulajdonságokkal rendelkezik, amelyek a képlet közvetlen következményei poláris formában: ${\ displaystyle \ mathbb {C} -\ mathbb {R} _ {\ leq 0}}$

Körök a Z -sík középpontú 0 vannak leképezve függőleges szegmensek a w -sík összekötő egy - πi , hogy egy + πi , ahol egy az igazi napló a kör sugara.
A z -sík 0 -ból sugárzó sugarai a w -sík vízszintes vonalaihoz vannak leképezve .

A z -síkban minden kör és sugár a fentiek szerint derékszögben találkozik. A Log alatt megjelenő képeik egy függőleges szegmens és egy vízszintes vonal (ill.) A w -síkban, és ezek is derékszögben találkoznak. Ez a Log konformális tulajdonságának illusztrációja.

A hozzá tartozó Riemann -felület

A log z Riemann -felületének vizualizációja . Úgy tűnik, hogy a felület a komplex sík eredetének megfelelő függőleges vonal körül spirálozik. A tényleges felület tetszőlegesen messzire nyúlik vízszintesen és függőlegesen is, de ezen a képen le van vágva.

Építkezés

A $log z$ különböző ágai nem ragaszthatók egyetlen folytonos függvényhez, mert két ág különböző értékeket adhat egy olyan ponton, ahol mindkettő definiálva van. Összehasonlítása, például a fő ág $Log ($ $z$ $)$ a képzeletbeli része $θ$ a $(-$ $π$ $,$ $π$ $)$ és az ág $L$ $($ $Z$ $)$ a amelynek képzetes rész $θ$ rejlik $(0,2$ $π$ $)$ . Ezek megegyeznek a felső félsíkon , de nem az alsó félsíkon. Tehát van értelme ezeknek az ágaknak a tartományait csak a felső félsík másolatai mentén ragasztani . A kapott ragasztott tartomány össze van kötve, de két példánya van az alsó félsíkról. Ez a két példány egy parkolóház két szintjeként vizualizálható, és az egyik az alsó félsík naplószintjétől az alsó félsík L szintjéig érhető el, ha $360 ° -kal az$ óramutató járásával ellentétesen $0$ körül mozog , először átlépve a pozitív valós tengelyt (a $napló$ szintjének) a felső félsík közös másolatába, majd keresztezi a negatív valós tengelyt (az $L$ szint) az alsó félsík $L$ szintjébe. ${\ displaystyle \ log \ kettőspont \ mathbb {C} ^{*} \ to \ mathbb {C}}$ ${\ displaystyle \ mathbb {C} -\ mathbb {R} _ {\ leq 0}}$ ${\ displaystyle \ mathbb {C} -\ mathbb {R} _ {\ geq 0}}$

Egy továbbra is ragasztással fiókok képzetes része $θ$ a $(π, 3 π)$ , a $(2 π, 4 π)$ , és így tovább, és a másik irányba, ágak képzetes része $θ$ a $(-2 π, 0)$ , in $(-3 π, - π)$ , és így tovább. A végeredmény egy összekapcsolt felület, amely spirális parkolóháznak tekinthető, végtelen sok szinttel felfelé és lefelé egyaránt. Ez a Riemann-felület $R$ kapcsolódó $log z$ .

Az $R$ pont egy párra $(z, θ) tekinthető,$ ahol $θ$ a $z$ argumentum lehetséges értéke . Ily módon $R$ beágyazható . ${\ displaystyle \ mathbb {C} \ times \ mathbb {R} \ kb \ mathbb {R} ^{3}}$

A logaritmus függvény a Riemann felületen

Mivel az ágak tartományait csak nyitott halmazok mentén ragasztották, ahol értékeik megegyeztek, az ágak ragasztva egyetlen jól definiált funkciót kapnak . Az R minden egyes pontját ( z , θ ) leképezi ln | -ig z | + iθ . Az eredeti Log napló kiterjesztésének folyamata kompatibilis holomorf függvények ragasztásával analitikus folytatásként ismert . ${\ displaystyle \ log _ {R} \ kettőspont R \ to \ mathbb {C}}$

Van egy "vetítési térkép" R -től lefelé, amely "lelapítja" a spirált, és elküldi ( z , θ ) a z -be . Bármelyik esetében , ha valaki felveszi R összes pontját ( z , θ ), amelyek "közvetlenül a z " felett helyezkednek el, és kiértékeli az _R logot ezeken a pontokon, akkor megkapja z összes logaritmusát . ${\ displaystyle \ mathbb {C} ^{*}}$ ${\ displaystyle z \ in \ mathbb {C} ^{*}}$

A log z összes ágának ragasztása

Ahelyett, hogy csak a fent kiválasztott ágakat ragasztaná, kezdheti a log z összes ágával , és egyidejűleg ragaszthat fel minden ágpárt és a legnagyobb nyílt részhalmaz mentén , amelyről L ₁ és L ₂ megegyezik. Ez eredményez ugyanolyan Riemann-felület R és a funkció log _R , mint korábban. Ez a megközelítés, bár némileg nehezebben vizualizálható, természetesebb, mivel nem igényel külön ágak kiválasztását. ${\ displaystyle L_ {1} \ kettőspont U_ {1} \ to \ mathbb {C}}$ ${\ displaystyle L_ {2} \ kettőspont U_ {2} \ to \ mathbb {C}}$ ${\ displaystyle U_ {1} \ cap U_ {2}}$

Ha U "egy nyílt részhalmaza R kiálló bijectively Arculatának U ben , majd a korlátozás a log _R , hogy U " megfelel egy ága log Z definiált U . A log z minden ága így keletkezik. ${\ displaystyle \ mathbb {C} ^{*}}$

A Riemann felület univerzális borításként

A vetítés térképen is tudatában R mint amely teret a . Valójában ez egy Galois -burkolat, amelyhez izomorf fedélzeti transzformációs csoport tartozik , amelyet a ( z , θ ) - ( z , θ +2 π ) küldő homeomorfizmus generál . ${\ displaystyle R \ to \ mathbb {C} ^{*}}$ ${\ displaystyle \ mathbb {C} ^{*}}$ ${\ displaystyle \ mathbb {Z}}$

Mint egy bonyolult sokaság , R jelentése biholomorphic azzal keresztül log _R . (Az inverz térkép küld Z az ( e ^z , Im z ).) Ez azt mutatja, hogy az R egyszerűen csatlakoztatva, így R jelentése az egyetemes fedelét a . ${\ displaystyle \ mathbb {C}}$ ${\ displaystyle \ mathbb {C} ^{*}}$

Alkalmazások

A komplex logaritmus szükséges a hatványozás meghatározásához , amelyben az alap egy komplex szám. Nevezetesen, ha $a$ és $b$ komplex számok $a \neq 0$ -val, akkor $a$ $főérték$ segítségével meghatározható $a b = e b Log a$ . Egy is helyettesítheti $Belépés a$ más logaritmusát $a$ megszerzése más értékeit $a b$ , illetve a különböző tényezők az űrlap $e 2π inb$ . Az $a b$ kifejezésnek csak akkor van értéke, ha $b$ egész szám.
Mivel a trigonometriai függvények az $e$ $iz$ racionális függvényeiként fejezhetők ki , az inverz trigonometrikus függvények összetett logaritmusokban fejezhetők ki.
Mivel a $w = Log z$ leképezés a $0$ középpontú köröket függőleges egyenes szegmensekké alakítja át, ez hasznos egy gyűrűt tartalmazó mérnöki alkalmazásokban .

Általánosítások

Logaritmusok más bázisokhoz

A valós számokhoz hasonlóan a b és az x összetett számokhoz is definiálható

{\ displaystyle \ log _ {b} x = {\ frac {\ log x} {\ log b}},}

azzal az egyetlen fenntartással, hogy értéke függ a b és x pontban meghatározott naplóág választásától (log b ≠ 0). Például a főérték használata megadja

{\ displaystyle \ log _ {i} e = {\ frac {\ operatornév {Log} e} {\ operatorname {Log} i}} = {\ frac {1} {\ pi i/2}} =-{\ frac {2i} {\ pi}}.}

Holomorf függvények logaritmusai

Ha f egy Holomorf függvény egy csatlakoztatott nyitott részhalmaza U a , majd egy ága log f a U egy folytonos függvény g az U úgy, hogy az e ^g⁽^Z⁾ = f ( z ) az összes z a U . Egy ilyen g függvény szükségszerűen holomorf, és g ′ ( z ) = f ′ ( z )/ f ( z ) minden z esetén U -ban . ${\ displaystyle \ mathbb {C}}$

Ha U egy egyszerűen csatlakoztatva nyitott részhalmaza , és F jelentése egy sehol-eltűnő Holomorf funkciót U , majd egy ága log f definiált U lehet kialakítani választásával kiindulási pont egy a U , kiválasztják a logaritmusa b a F ( a ), és meghatározása ${\ displaystyle \ mathbb {C}}$

{\ displaystyle g (z) = b+\ int _ {a}^{z} {\ frac {f '(w)} {f (w)}} \, dw}