Hypergráf - Hypergraph

Példa egy irányítatlan hipergráfra, és . Ennek a hipergráfnak sorrendje 7 és mérete 4. Itt az élek nem csak két csúcsot, hanem több csúcsot kötnek össze, és színekkel ábrázolják.${\ displaystyle X = \ {v_ {1}, v_ {2}, v_ {3}, v_ {4}, v_ {5}, v_ {6}, v_ {7} \}}$${\ displaystyle E = \ {e_ {1}, e_ {2}, e_ {3}, e_ {4} \} =}$ ${\ displaystyle \ {\ {v_ {1}, v_ {2}, v_ {3} \},}$ ${\ displaystyle \ {v_ {2}, v_ {3} \},}$ ${\ displaystyle \ {v_ {3}, v_ {5}, v_ {6} \},}$ ${\ displaystyle \ {v_ {4} \} \}}$

A fenti ábrán bemutatott hipergráf alternatív ábrázolása, PAOH. Az élek függőleges vonalak, amelyek összekötik a csúcsokat. V7 egy elszigetelt csúcs. A csúcsok balra vannak igazítva. A jobb oldali felirat mutatja az élek nevét.

Példa egy irányított hipergráfra, és .${\ displaystyle X = \ {1,2,3,4,5,6 \}}$${\ displaystyle E = \ {a_ {1}, a_ {2}, a_ {3}, a_ {4}, a_ {5} \} =}$ ${\ displaystyle \ {(\ {1 \}, \ {2 \}),}$ ${\ displaystyle (\ {2 \}, \ {3 \}),}$ ${\ displaystyle (\ {3 \}, \ {1 \}),}$ ${\ displaystyle (\ {2,3 \}, \ {4,5 \}),}$ ${\ displaystyle (\ {3,5 \}, \ {6 \}) \}}$

A matematikában a hipergráf egy gráf általánosítása, amelyben egy él tetszőleges számú csúcshoz csatlakozhat . Ezzel szemben egy közönséges gráfban egy él pontosan két csúcsot köt össze.

Formailag az irányítatlan hipergráf olyan pár, ahol csomópontoknak vagy csúcsoknak nevezett elemek halmaza , és (irányítatlan hipergráfban) nem üres részhalmazok halmaza, amelyeket hiperhivatkozásoknak vagy éleknek neveznek . Ezért egy részhalmaza , ahol a áramfejlesztőt az . A csúcshalmaz méretét a hipergráf sorrendjének nevezzük, az élek halmazának pedig a hipergráf méretét . ${\ displaystyle H}$${\ displaystyle H = (X, E)}$${\ displaystyle X}$${\ displaystyle E}$${\ displaystyle X}$${\ displaystyle E}$${\ displaystyle {\ mathcal {P}} (X) \ setminus \ {\ emptyyset \}}$${\ displaystyle {\ mathcal {P}} (X)}$${\ displaystyle X}$

Az irányított hipergráf abban különbözik egymástól, hogy hipergombjai nem halmazok, hanem annak rendezett pár részhalmazai , amelyek a hiperedge farkát és fejét alkotják. ${\ displaystyle X}$

Míg a gráf élei csak 2 csomópontot kötnek össze, a hipergerendák tetszőleges számú csomópontot kötnek össze. Mindazonáltal gyakran kívánatos olyan hipergráfok tanulmányozása, ahol az összes hiperág azonos kardinalitással rendelkezik; A k-egyenletes hipergráf olyan hipergráf, amely minden hipergegrája k méretű . (Más szóval, az egyik ilyen hipergráf halmazok gyűjteménye, minden ilyen halmaz egy hiperág, amely összeköti a k csomópontokat.) Tehát a 2-egyenletes hipergráf egy gráf, a 3-egyenletes hipergráf a rendezetlen hármasok gyűjteménye stb. Irányítatlan hipergráfra is hívják beállított rendszer vagy egy család készletek levonni a alaphalmaz .

A hipergráfok előfordulási struktúrának tekinthetők . Különösen létezik egy kétoldalú "incidenciagráf" vagy " Levi -gráf ", amely minden hipergráfnak megfelel, és fordítva, a legtöbb, de nem minden kétoldalú gráf tekinthető a hipergráfok előfordulási grafikonjainak.

A hipergráfoknak sok más neve is van. A számítási geometriában az irányítatlan hipergráfot néha tartománytérnek nevezhetjük , majd a hiperrajzokat tartományoknak . A kooperatív játékelméletben a hipergráfokat egyszerű játékoknak (szavazójátékok) nevezik ; ezt a fogalmat a társadalmi választás elméletének problémáinak megoldására alkalmazzák . Egyes szakirodalmakban a széleket hiperhivatkozásoknak vagy összekötőknek nevezik .

A gyűjtemény hipergráfokon egy kategória a hipergráfra homomorphisms mint morfizmusok .

Alkalmazások

Az irányítatlan hipergráfok hasznosak olyan modellezéseknél, mint a kielégítési problémák, adatbázisok, gépi tanulás és Steiner -faproblémák . Ezeket széles körben alkalmazták a gépi tanulási feladatokban, mint adatmodell és osztályozó rendszeresítés (matematika) . Az alkalmazások magukban foglalják az ajánlórendszert (közösségek, mint hipergerek), képvisszanyerést (korrelációk, mint hyperedges) és a bioinformatikát (biokémiai kölcsönhatások, mint hyperedges). A reprezentatív hipergráf tanulási technikák közé tartozik a hipergráf spektrális csoportosítás, amely kiterjeszti a spektrális gráfelméletet a hipergráf Laplacianusra, és a hipergráf félig felügyelt tanulás , amely extra hipergráf strukturális költségeket vezet be a tanulási eredmények korlátozására. Nagyméretű hipergráfokhoz az Apache Spark használatával felépített elosztott keretrendszer is rendelkezésre áll.

Az irányított hipergráfok felhasználhatók olyan dolgok modellezésére, mint a telefonos alkalmazások, a pénzmosás felderítése , a műveletek kutatása és a szállítás tervezése. Használhatók a Horn-kielégíthetőség modellezésére is .

A fogalmak általánosítása grafikonokból

Sok tétel és fogalom, amelyek gráfokat tartalmaznak, a hipergráfokra is érvényesek, különösen:

• Egyezés hipergráfokban ;
• Csúcsborítás hipergráfokban (más néven: keresztirányú );
• Vonal grafikon egy hipergráfban ;
• Hipergráf nyelvtan - a hipergráfok osztályának kiegészítésével létrehozott helyettesítési szabályokkal;
• Ramsey tétele ;
• Erdős – Ko – Rado -tétel ;
• Kruskal – Katona -tétel az egyenletes hipergráfokról;
• Hall típusú tételek hipergráfokhoz .

Irányított hipergráfokban: tranzitív lezárás és legrövidebb út problémák.

Hypergraph rajz

Ez az áramköri rajz egy hipergráf rajzaként értelmezhető, amelyben négy csúcsot (fehér téglalapként és korongként ábrázolva) három, fákként rajzolt hiperrajz köt össze.

Bár a hipergráfokat nehezebb papírra rajzolni, mint a grafikonokat, több kutató tanulmányozta a hipergráfok megjelenítésének módszereit.

A hipergráfok egyik lehetséges vizuális ábrázolásában, hasonlóan a szokásos gráfrajzolási stílushoz, amelyben a síkban lévő görbéket használják a gráf éleinek ábrázolására, a hipergráf csúcsait pontok, lemezek vagy dobozok, a hipergráfokat pedig fákként ábrázolják. a csúcsokat, mint leveleiket. Ha a csúcsokat pontokként ábrázoljuk, akkor a hiperhéjak sima görbékként is megjelenhetnek, amelyek összekötik a pontok halmazait, vagy egyszerű zárt görbékként , amelyek pontok halmazát zárják le.

Egy 4-es rendű Venn-diagram, amely úgy értelmezhető, mint egy hipergráf felosztási rajza, amely 15 csúcsot (a 15 színes területet) és 4 hipergemet (a 4 ellipszist) tartalmaz.

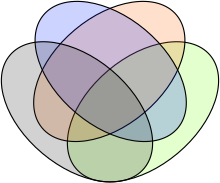
A hipergráf vizualizáció egy másik stílusában, a hipergráfrajz alosztási modelljében a sík régiókra van osztva, amelyek mindegyike a hipergráf egyetlen csúcsát képviseli. A hipergráf hipergombjait e régiók összefüggő részhalmazai képviselik, amelyeket színezés, körvonalak rajzolása vagy mindkettő jelezhet. Például egy n-es rendű Venn-diagramot úgy tekinthetünk, mint egy hipergráf felosztási rajzát, amelyben n hyperedge (a diagramot meghatározó görbék) és 2 ^n-  1 csúcs található (azokat a régiókat ábrázolva, amelyekbe ezek a görbék felosztják a síkot). A síkgráfok polinomiális idejű felismerésével ellentétben NP-teljességgel meg lehet határozni , hogy van - e egy hipergráf sík felosztási rajza, de az ilyen típusú rajzok létezése hatékonyan tesztelhető, ha a régiók szomszédsági mintázata korlátozott. hogy út, ciklus vagy fa legyen.

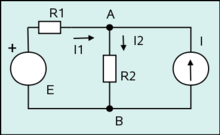
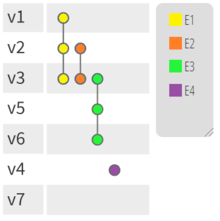
A PAOH nevű hipergráf alternatív ábrázolása a cikk tetején található ábrán látható. Az élek függőleges vonalak, amelyek összekötik a csúcsokat. A csúcsok balra vannak igazítva. A jobb oldali felirat mutatja az élek nevét. Dinamikus hipergráfokhoz tervezték, de egyszerű hipergráfokhoz is használható.

Hypergraph színezés

A klasszikus hipergráf színezés az egyik szín hozzárendelése a halmazból a hipergráf minden csúcsához oly módon, hogy minden hiperrajz legalább két különböző színű csúcsot tartalmaz. Más szavakkal, nem lehet monokromatikus hiperge, legalább 2 -es számossággal. Ebben az értelemben ez a grafikon színezésének általános általánosítása. A használt színek minimális számát minden színezésen hipergráf kromatikus számának nevezzük. ${\ displaystyle \ {1,2,3, ... \ lambda \}}$

Azokat a hipergráfokat, amelyekhez legfeljebb k színt alkalmazó színezés létezik , k-színezhetőnek nevezzük . A 2 színezhető hipergráf pontosan a kétoldalú.

A klasszikus hipergráf színezés sok általánosítást tartalmaz. Az egyik az úgynevezett vegyes hipergráf-színezés, amikor a monokromatikus élek megengedettek. Néhány vegyes hipergráf nem színezhető bármilyen számú szín esetén. A színtelenség általános kritériuma ismeretlen. Ha a vegyes hipergráf színezhető, akkor a használt színek minimális és maximális számát nevezzük alsó és felső kromatikus számnak. A részletekért lásd: http://spectrum.troy.edu/voloshin/mh.html .

A hipergráfok tulajdonságai

A hipergráf különféle tulajdonságokkal rendelkezhet, például:

• Üres - nincs éle.
• Nem egyszerű (vagy több ) - hurkokkal (egyetlen csúcsú hipergerendákkal) vagy ismételt élekkel rendelkezik, ami azt jelenti, hogy két vagy több él is tartalmazhat azonos csúcshalmazt.
• Egyszerű - nincs hurok és nincs ismételt éle.
• ${\ displaystyle d}$-reguláris - minden csúcsnak van foka , azaz pontosan hipergerek.${\ displaystyle d}$${\ displaystyle d}$
• 2 -színezhető - csúcsai két U és V osztályra oszthatók oly módon, hogy minden, legalább 2 -es kardinalitással rendelkező hiperág tartalmazjon legalább egy csúcsot mindkét osztályból. Alternatív kifejezés a B tulajdonság .
  • Két erősebb tulajdonság a kétoldalú és kiegyensúlyozott .
• ${\ displaystyle k}$-egységes - minden hiperge pontosan csúcsokat tartalmaz .${\ displaystyle k}$
• ${\ displaystyle k}$-partite - a csúcsok részekre vannak osztva , és minden hiperhéj pontosan egy csúcsot tartalmaz minden típusból. ${\ displaystyle k}$
  • Minden -partite hipergráfra (a ) mind -egységes és kétoldalú (2-színezhető).${\ displaystyle k}$${\ displaystyle k \ geq 2}$${\ displaystyle k}$
• Lefelé zárva - az irányítatlan hipergráf széleinek minden részhalmaza hiperge. A lefelé zárt hipergráfot általában elvont egyszerű komplexnek nevezik .
  • Egy absztrakt egyszerű komplexumot egy további tulajdonsággal, amelyet augmentációs tulajdonságnak neveznek, matroidnak nevezzük .

Kapcsolódó hipergráfok

Mivel a hipergráf -linkek bármilyen kardinalitást is tartalmazhatnak, az algráf fogalmának több fogalma is létezik, amelyeket alhipergráfoknak , részleges hipergráfoknak és szakasz -hipergráfoknak neveznek .

Legyen a csúcsokból álló hipergráf ${\ displaystyle H = (X, E)}$

${\ displaystyle X = \ lbrace x_ {i} \ mid i \ in I_ {v} \ rbrace,}$

és az él beállítva

${\ displaystyle E = \ lbrace e_ {i} \ mid i \ in I_ {e} \ land e_ {i} \ subseteq X \ land e_ {i} \ neq \ emptyyset \ rbrace,}$

ahol és a index készlet a csúcsok és élek ill. ${\ displaystyle I_ {v}}$${\ displaystyle I_ {e}}$

Az alhipergráf olyan hipergráf, amelynek néhány csúcsa el van távolítva. Formálisan az által indukált alhipergráf a következőképpen van definiálva ${\ displaystyle H_ {A}}$${\ displaystyle A \ subseteq X}$

${\ displaystyle H_ {A} = \ left (A, \ lbrace e \ cap A \ mid e \ in E \ land e \ cap A \ neq \ emptyyset \ rbrace \ right).}$

Egy alternatív kifejezés a korlátozása H a A .

Az alhipergráf kiterjesztése olyan hipergráf, ahol minden hipergráf részlegesen benne van az alhipergráfban , teljes egészében benne van a kiterjesztésben . Formálisan ${\ displaystyle H}$${\ displaystyle H_ {A}}$${\ displaystyle Ex (H_ {A})}$

${\ displaystyle Ex (H_ {A}) = (A \ cup A ', E')}$A és .${\ displaystyle A '= \ bigcup _ {e \ in E} e \ setminus A}$${\ displaystyle E '= \ lbrace e \ in E \ mid e \ subseteq (A \ cup A') \ rbrace}$

A részleges hipergráf olyan hipergráf, amelynek néhány éle eltávolítva van. Az élindexkészlet egy részhalmaza miatt a részleges hipergráf a hipergráf ${\ displaystyle J \ I_ részhalmaz {e}}$${\ displaystyle J}$

${\ displaystyle \ left (X, \ lbrace e_ {i} \ mid i \ in J \ rbrace \ right).}$

Adott egy részhalmaz , a szakasz hipergráf a részleges hipergráf ${\ displaystyle A \ subseteq X}$

${\ displaystyle H \ times A = \ left (A, \ lbrace e_ {i} \ mid i \ in I_ {e} \ land e_ {i} \ subseteq A \ rbrace \ right).}$

A kettős a jelentése hipergráfra amelynek csúcsai és élei vannak cserélve, így a csúcsok által adott és amelynek szélei vannak megadva , ahol ${\ displaystyle H^{*}}$${\ displaystyle H}$${\ displaystyle \ lbrace e_ {i} \ rbrace}$${\ displaystyle \ lbrace X_ {m} \ rbrace}$

${\ displaystyle X_ {m} = \ lbrace e_ {i} \ mid x_ {m} \ in e_ {i} \ rbrace.}$

Ha az egyenlőség fogalmát megfelelően definiáljuk, az alábbiak szerint, akkor a hipergráf duáljának felvételének művelete involúció , azaz

${\ displaystyle \ left (H^{*} \ right)^{*} = H.}$

Egy gráf G ugyanazzal csúcshalmaza, mint a csatlakoztatott hipergráf H egy fogadó grafikon a H , ha minden hiperél a H indukál egy csatlakoztatott részgráfot a G . Szétkapcsolt hipergráf H , G egy fogadó gráf, ha van egy bijekciót között csatlakoztatott komponensek a G és H , úgy, hogy mindegyik csatlakoztatott komponens a G „ a G egy gazdasejt a megfelelő H” .

A 2-szakasz (vagy klikk grafikon , ami grafikon , ősi grafikon , Gaifman grafikon ) egy hipergráf a grafikon az azonos csúcsai a hipergráf, és élek közötti összes pár csúcsot, amely ugyanazon hiperél.

Előfordulási mátrix

Hagyja és . Minden hipergráfnak van egy előfordulási mátrixa . ${\ displaystyle V = \ {v_ {1}, v_ {2}, ~ \ ldots, ~ v_ {n} \}}$${\ displaystyle E = \ {e_ {1}, e_ {2}, ~ \ ldots ~ e_ {m} \}}$${\ displaystyle n \ x m}$

Irányítatlan hipergráfhoz, ahol ${\ displaystyle I = (b_ {ij})}}$

${\ displaystyle b_ {ij} = \ left \ {{\ begin {mátrix} 1 & \ mathrm {if} ~ v_ {i} \ in e_ {j} \\ 0 & \ mathrm {egyébként}. \ end {mátrix}} \jobb.}$

A transzponáltját az előfordulási mátrix határozza meg a hipergráf úgynevezett kettős az , ahol egy m -element készlet és egy n -element halmaza részhalmazainak . Akkor és csak akkor, ha . ${\ displaystyle I^{t}}$${\ displaystyle H^{*} = (V^{*}, \ E^{*})}$${\ displaystyle H}$${\ displaystyle V^{*}}$${\ displaystyle E^{*}}$${\ displaystyle V^{*}}$${\ displaystyle v_ {j}^{*} \ in V^{*}}$${\ displaystyle e_ {i}^{*} \ in E^{*}, ~ v_ {j}^{*} \ in e_ {i}^{*}}$ ${\ displaystyle b_ {ij} = 1}$

Irányított hipergráf esetén az egyes hipergerek fejét és farkát jelöli és . ahol ${\ displaystyle e_ {j}}$${\ displaystyle H (e_ {j})}$${\ displaystyle T (e_ {j})}$${\ displaystyle I = (b_ {ij})}}$

${\ displaystyle b_ {ij} = \ left \ {{\ begin {mátrix} -1 & \ mathrm {if} ~ v_ {i} \ in T (e_ {j}) \\ 1 & \ mathrm {if} ~ v_ { i} \ in H (e_ {j}) \\ 0 & \ mathrm {egyébként}. \ end {mátrix}} \ jobb.}$

Előfordulási grafikon

A hipergráf H képviselheti egy páros gráf BG a következőképpen: a készletek X és E jelentése a partíciókat a BG , és ( x ₁ , e ₁ ) vannak csatlakoztatva egy éllel, ha, és csak akkor, ha vertex x ₁ tartalmazza szélén e ₁ a H -ban .

Ezzel szemben minden olyan kétoldalú gráf, amelynek rögzített részei vannak, és nincsenek összekapcsolt csomópontok a második részben, valamilyen hipergráfot jelent a fent leírt módon. Ezt a kétoldalú gráfot előfordulási gráfnak is nevezik .

Szomszédsági mátrix

A hipergráf szomszédsági mátrixával párhuzam vonható le a gráf szomszédsági mátrixából . Egy gráf esetében a szomszédsági mátrix egy négyzet mátrix, amely azt jelzi, hogy a csúcspárok szomszédosak -e . Hasonlóképpen definiálhatjuk a szomszédsági mátrixot általában egy hipergráfhoz, ahol a hipergerek valódi súlyokkal rendelkeznek ${\ displaystyle A = (a_ {ij})}}$${\ displaystyle e_ {k \ leq m}}$${\ displaystyle w_ {e_ {k}} \ in \ mathbb {R}}$

${\ displaystyle a_ {ij} = \ left \ {{\ begin {mátrix} w_ {e_ {k}} & \ mathrm {if} ~ (v_ {i}, v_ {j}) \ in E \\ 0 & \ mathrm {egyébként}. \ end {mátrix}} \ jobb.}$

Ciklusok

Ellentétben a közönséges irányítatlan gráfokkal, amelyeknek egyetlen természetes fogalma van a ciklusokról és az aciklikus gráfokról , az aciklikusságnak több természetes, nem egyenértékű definíciója van a hipergráfok esetében, amelyek a közönséges gráfok különleges esetére a normál gráf aciklikusságára omlanak össze.

A hipergráfok aciklikusságának első meghatározását Claude Berge adta meg : a hipergráf akkor Berge-aciklikus, ha előfordulási grafikonja (a fent definiált kétoldalú gráf ) aciklikus. Ez a meghatározás nagyon korlátozó: például, ha egy hipergráfnak van pár csúcsa és néhány pár hiperhíre, és akkor Berge-ciklikus. A Berge-ciklikusság nyilvánvalóan lineáris időben tesztelhető az incidenciagráf feltárásával. ${\ displaystyle v \ neq v '}$${\ displaystyle f \ neq f '}$${\ displaystyle v, v '\ in f}$${\ displaystyle v, v '\ in f'}$

Meghatározhatjuk a hipergráf aciklikusság gyengébb fogalmát, amelyet később α-aciklikusságnak nevezünk. Az aciklikusságnak ez a fogalma egyenértékű azzal, hogy a hipergráf konform (a primer gráf minden klikkét valamilyen hipergörbe borítja), és primális gráfja akkordos ; a GYO algoritmuson (más néven Graham -algoritmuson) keresztül történő redukálhatósággal egyenértékű az üres gráffal való redukálhatósággal is, amely egy összefolyó iteratív folyamat, amely a fülek általános definíciója alapján eltávolítja a hiperjeleket . Az adatbázis-elmélet területén ismert, hogy az adatbázis-séma bizonyos kívánatos tulajdonságokkal rendelkezik, ha a mögöttes hipergráf α-aciklikus. Emellett, α-acyclia is kapcsolódik a kifejező a őrzött fragmens az elsőrendű logika .

Lineáris idő alatt tesztelhetjük, hogy a hipergráf α-aciklikus.

Ne feledje, hogy az α-aciklikusságnak megvan az intuitív tulajdonsága, hogy a hipergerek hozzáadása az α-ciklikus hipergráfhoz α-aciklikussá teheti (például a hipergráf minden csúcsát tartalmazó hiperág hozzáadásával mindig α-aciklikus lesz). Ronald Fagin , részben ennek az észlelt hiányosságnak a motivációjával határozta meg a β-aciklusosság és a γ-aciklusosság erősebb fogalmát. Megállapíthatjuk a β-aciklusosságot, mint azt a követelményt, hogy a hipergráf összes alhipergráfja α-aciklusos legyen, ami egyenértékű Graham korábbi definíciójával. A γ-aciklusosság fogalma korlátozóbb feltétel, amely az adatbázis-sémák számos kívánatos tulajdonságával egyenértékű, és a Bachman-diagramokhoz kapcsolódik . A β-aciklusosság és a γ-aciklusosság polinomiális időben is tesztelhető .

Az aciklikusságnak ez a négy fogalma összehasonlítható: a Berge-aciklusosság γ-aciklusosságot jelent, ami β-aciklusosságot, ami α-aciklusosságot is magában foglal. A fordított következmények egyike sem állja meg a helyét, ezért ez a négy fogalom eltérő.

Izomorfizmus, szimmetria és egyenlőség

A hipergráf -homomorfizmus egy térkép az egyik hipergráf csúcshalmazából a másikba úgy, hogy minden él egy másik élhez térképezzen.

A hipergráfot az izomorf egy hipergráfban írja le, mint ha létezik olyan bijekciót${\ displaystyle H = (X, E)}$${\ displaystyle G = (Y, F)}$${\ displaystyle H \ simeq G}$

${\ displaystyle \ phi: X \ Y}$

és a permutáció az , hogy ${\ displaystyle \ pi}$${\ displaystyle I}$

${\ displaystyle \ phi (e_ {i}) = f _ {\ pi (i)}}$

A bikciót ekkor gráfok izomorfizmusának nevezik . Vegye figyelembe, hogy ${\ displaystyle \ phi}$

${\ displaystyle H \ simeq G}$ha és csak akkor .${\ displaystyle H^{*} \ simeq G^{*}}$

Ha a hipergráf széleit kifejezetten megcímkézik, akkor az erős izomorfizmus további fogalma . Az egyik azt mondja, hogy az erősen izomorf hogy ha a permutáció a személyazonosságát. Az egyik aztán ír . Vegye figyelembe, hogy minden erősen izomorf gráf izomorf, de nem fordítva. ${\ displaystyle H}$${\ displaystyle G}$${\ displaystyle H \ cong G}$

Ha a hipergráf csúcsait kifejezetten megcímkézik, akkor az egyenértékűség és az egyenlőség fogalma is megjelenik . Az egyik azt mondja, hogy ez egyenértékű a , és azt írta , ha a izomorfizmus van ${\ displaystyle H}$${\ displaystyle G}$${\ displaystyle H \ equiv G}$${\ displaystyle \ phi}$

${\ displaystyle \ phi (x_ {n}) = y_ {n}}$

és

${\ displaystyle \ phi (e_ {i}) = f _ {\ pi (i)}}$

Vegye figyelembe, hogy

${\ displaystyle H \ equiv G}$ ha, és csak akkor ha ${\ displaystyle H^{*} \ cong G^{*}}$

Ha ezenkívül a permutáció az identitás, akkor azt mondja, hogy egyenlő , és ír . Ne feledje, hogy az egyenlőség ezen meghatározásával a gráfok önmaguk kettősek: ${\ displaystyle \ pi}$${\ displaystyle H}$${\ displaystyle G}$${\ displaystyle H = G}$

${\ displaystyle \ left (H^{*} \ right)^{*} = H}$

A hipergráf -automorfizmus olyan izomorfizmus, amely egy önmagából beállított csúcsból származik, vagyis a csúcsok átcímkézése. A H (= ( X ,  E )) hipergráf automorfizmusainak halmaza egy összetétel alatt álló csoport , amelyet a hipergráf és az Aut ( H ) írásbeli automorfizmus csoportjának neveznek .

Példák

Tekintsük a szélekkel rendelkező hipergráfot${\ displaystyle H}$

${\ displaystyle H = \ lbrace e_ {1} = \ lbrace a, b \ rbrace, e_ {2} = \ lbrace b, c \ rbrace, e_ {3} = \ lbrace c, d \ rbrace, e_ {4} = \ lmerevítő d, a \ rfűző, e_ {5} = \ lmerevítő b, d \ rheveder, e_ {6} = \ lmerevítő a, c \ rhegyzet \ rbrace}$

és

${\ displaystyle G = \ lbrace f_ {1} = \ lbrace \ alpha, \ beta \ rbrace, f_ {2} = \ lbrace \ beta, \ gamma \ rbrace, f_ {3} = \ lbrace \ gamma, \ delta \ rbrace, f_ {4} = \ lbrace \ delta, \ alpha \ rbrace, f_ {5} = \ lbrace \ alpha, \ gamma \ rbrace, f_ {6} = \ lbrace \ beta, \ delta \ rbrace \ rbrace}$

Akkor egyértelműen és izomorf (a , stb ), de nem erősen izomorfak. Így például a -ban a csúcs találkozik az 1 -es , 4 -es és 6 -os élekkel, így ${\ displaystyle H}$${\ displaystyle G}$${\ displaystyle \ phi (a) = \ alpha}$${\ displaystyle H}$${\ displaystyle a}$

${\ displaystyle e_ {1} \ cap e_ {4} \ cap e_ {6} = \ lbrace a \ rbrace}$

A gráfban nincs olyan csúcs, amely megfelel az 1, 4 és 6 éleknek: ${\ displaystyle G}$

${\ displaystyle f_ {1} \ cap f_ {4} \ cap f_ {6} = \ varnothing}$

Ebben a példában, és egyenértékűek, és a duals erősen izomorf: . ${\ displaystyle H}$${\ displaystyle G}$${\ displaystyle H \ equiv G}$${\ displaystyle H^{*} \ cong G^{*}}$

Szimmetria

Az a hipergráf rangja a hipergráfbármelyik élének maximális számossága. Ha minden élekazonos, akkor a hipergráfegységesvagyk-egységes, vagyk-hipergráfnaknevezik. A gráf csak két egyenletes hipergráf. ${\ displaystyle r (H)}$${\ displaystyle H}$

A mértéke d (v) egy csúcs v az élek számát, amelyek tartalmazzák azt. H a k-reguláris , ha minden csúcs foka k .

Az egységes hipergráf kettős szabályos és fordítva.

Két csúcsot x és y a H nevezzük szimmetrikus , ha létezik olyan automor olyan, hogy . Két éle, és szimmetrikusnak mondható, ha létezik olyan automorfizmus, hogy . ${\ displaystyle \ phi (x) = y}$${\ displaystyle e_ {i}}$${\ displaystyle e_ {j}}$${\ displaystyle \ phi (e_ {i}) = e_ {j}}$

A hipergráfot akkor mondjuk csúcs-tranzitívnek (vagy csúcsszimmetrikusnak ), ha minden csúcsa szimmetrikus. Hasonlóképpen a hipergráf él-tranzitív, ha minden éle szimmetrikus. Ha egy hipergráf mind él-, mind csúcsszimmetrikus, akkor a hipergráf egyszerűen tranzitív .

A hipergráf kettőssége miatt az él-tranzitivitás vizsgálata megegyezik a csúcs-tranzitivitás vizsgálatával.

Partíciók

Az E. Dauber miatti partíciótétel azt állítja, hogy egy él-tranzitív hipergráf esetében létezik egy partíció${\ displaystyle H = (X, E)}$

${\ displaystyle (X_ {1}, X_ {2}, \ cdots, X_ {K})}$

a csúcshalmazból úgy , hogy az által generált alhipergráf mindegyikre tranzitív , és olyan ${\ displaystyle X}$${\ displaystyle H_ {X_ {k}}}$${\ displaystyle X_ {k}}$${\ displaystyle 1 \ leq k \ leq K}$

${\ displaystyle \ sum _ {k = 1}^{K} r \ left (H_ {X_ {k}} \ right) = r (H)}$

hol van H rangja . ${\ displaystyle r (H)}$

Következésképpen az él-tranzitív hipergráf, amely nem vertex-tranzitív, kétszínű.

A gráfpartícionálás (és különösen a hipergráf particionálás) számos alkalmazást tartalmaz az IC tervezéshez és a párhuzamos számításhoz. A hatékony és skálázható hipergráf -particionáló algoritmusok szintén fontosak a nagyméretű hipergráfok feldolgozásakor a gépi tanulási feladatokban.

További általánosítások

A hipergráf egyik lehetséges általánosítása, hogy az élek más élekre mutathatnak. Ennek az általánosításnak két változata van. Az egyikben az élek nemcsak csúcshalmazból állnak, hanem tartalmazhatnak csúcsrészleteket, csúcsrészhalmazok részhalmazait és így tovább végtelenül . Lényegében minden él csak egy fa belső csomópontja vagy irányított aciklikus gráf , a csúcsok pedig a levélcsomópontok. A hipergráf ilyenkor csak a közös, közös csomópontú fák gyűjteménye (vagyis egy adott belső csomópont vagy levél több különböző fán is előfordulhat). Ezzel szemben minden fagyűjtemény ezen általánosított hipergráfként értelmezhető. Mivel a fákat széles körben használják az informatikában és a matematika számos más ágában, azt mondhatjuk, hogy a hipergráfok természetesen is megjelennek. Így például ez az általánosítás természetesen az algebra kifejezés modelljeként merül fel ; élek kifejezéseknek , csúcsok konstansoknak vagy változóknak felelnek meg.

Egy ilyen hipergráfhoz a halmaztagság rendelést ad, de a rendelés nem részleges vagy előrendelés , mivel nem tranzitív. Az általánosítás Levi gráfjának megfelelő gráf egy irányított aciklikus gráf . Vegyük például azt az általánosított hipergráfot, amelynek csúcshalmaza és éle az és . Akkor, bár és , ez nem igaz . Az ilyen hipergráfok halmaztagságának tranzitív lezárása azonban részleges sorrendet indukál , és a hipergráfot részlegesen rendezett halmazba "simítja" . ${\ displaystyle V = \ {a, b \}}$${\ displaystyle e_ {1} = \ {a, b \}}$${\ displaystyle e_ {2} = \ {a, e_ {1} \}}$${\ displaystyle b \ in e_ {1}}$${\ displaystyle e_ {1} \ in e_ {2}}$${\ displaystyle b \ in e_ {2}}$

Alternatív megoldásként az élek más élekre is mutathatnak, függetlenül attól a követelménytől, hogy az éleket rendeltetésszerűen aciklikus gráfok szerint kell rendezni. Ez lehetővé teszi az élhurkos gráfok használatát, amelyeknek egyáltalán nem kell csúcsokat tartalmazniuk. Tekintsük például az általánosított hipergráfot, amely két élből és , és nulla csúcsból áll, így és . Mivel ez a hurok végtelenül rekurzív, az élek halmazai megsértik az alapozás axiómáját . Különösen az ilyen hipergráfok esetében nincs átmeneti lezárása a halmaztagságnak. Bár az ilyen struktúrák elsőre furcsának tűnhetnek, könnyen megérthetők azzal, hogy megjegyzik, hogy Levi -gráfjuk egyenértékű általánosítása már nem kétoldalú , hanem csak egy általános irányított gráf . ${\ displaystyle e_ {1}}$${\ displaystyle e_ {2}}$${\ displaystyle e_ {1} = \ {e_ {2} \}}$${\ displaystyle e_ {2} = \ {e_ {1} \}}$

Az ilyen hipergráfok általános előfordulási mátrixa definíció szerint egy négyzet mátrix, amelynek rangja megegyezik a csúcsok és élek teljes számával. Így a fenti példában az előfordulási mátrix egyszerűen

${\ displaystyle \ left [{\ begin {mátrix} 0 & 1 \\ 1 & 0 \ end {mátrix}} \ right].}$

Lásd még

• Kombinatorikus kialakítás
• Faktográf
• Greedoid
• Előfordulás szerkezete
• Többgráf
• P rendszer
• Ritka mátrix-vektor szorzás

Megjegyzések

Hivatkozások

• Berge, Claude (1984). Hipergráfok: Véges halmazok kombinatorikája . Elsevier. ISBN 978-0-08-088023-5.
• Berge, C .; Ray-Chaudhuri, D. (2006). Hypergraph szeminárium: Ohio State University, 1972 . Előadás jegyzetek matematikából. 411 . Springer. ISBN 978-3-540-37803-7.
• "Hypergraph" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Bretto, Alain (2013). Hipergráf -elmélet: Bevezetés . Springer. ISBN 978-3-319-00080-0.
• Voloshin, Vitalij I. (2002). A vegyes hipergráfok színezése: elmélet, algoritmusok és alkalmazások: elmélet, algoritmusok és alkalmazások . Fields Intézet monográfiái. 17 . Amerikai Matematikai Társaság. ISBN 978-0-8218-2812-0.
• Voloshin, Vitalij I. (2009). Bevezetés a gráf és hipergráf elméletbe . Nova Science. ISBN 978-1-61470-112-5.
• Ez a cikk a PlanetMath hipergráfjának anyagát tartalmazza , amely a Creative Commons Hozzárendelési/megosztási licenc alapján licencelt .

Külső linkek

• PAOHVis : nyílt forráskódú PAOHVis rendszer dinamikus hipergráfok megjelenítésére.