Ljapunov kitevője - Lyapunov exponent

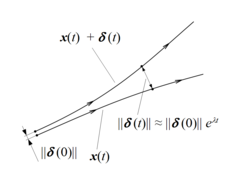
A matematika , a Ljapunov exponens vagy Lyapunov jellemző exponens egy dinamikus rendszer olyan mennyiség, amely jellemzi az elválasztási sebesség a végtelenségig közel pályákat . Mennyiségileg két pálya a fázistérben , kezdeti szeparációs vektorral eltér (feltéve, hogy az eltérés kezelhető a linearizált közelítésen belül) a ${\ displaystyle \ delta \ mathbf {Z} _ {0}}$

${\ displaystyle | \ delta \ mathbf {Z} (t) | \ kb e^{\ lambda t} | \ delta \ mathbf {Z} _ {0} |}$

hol van Ljapunov kitevője. ${\ displaystyle \ lambda}$

Az elválasztási sebesség eltérő lehet a kezdeti szeparációs vektor különböző irányaiban. Így létezik Liapunov -kitevők spektruma - számukban egyenlő a fázistér dimenziójával. Gyakori, hogy a legnagyobbat a legnagyobb Ljapunov -kitevőnek (MLE) nevezzük , mert ez meghatározza a dinamikus rendszer kiszámíthatóságának fogalmát . A pozitív MLE -t általában a rendszer kaotikus jelzésére kell tekinteni(feltéve, hogy bizonyos egyéb feltételek teljesülnek, pl. fázistér tömörség). Ne feledje, hogy egy tetszőleges kezdeti elválasztási vektor jellemzően tartalmaz néhány komponenst az MLE -hez kapcsolódó irányban, és az exponenciális növekedési ütem miatt a többi kitevő hatása idővel megszűnik.

A kitevő Aleksandr Ljapunov nevéhez fűződik .

A maximális Ljapunov -kitevő meghatározása

A maximális Ljapunov -kitevő a következőképpen határozható meg:

${\ displaystyle \ lambda = \ lim _ {t \ to \ infty} \ lim _ {| \ delta \ mathbf {Z} _ {0} | \ to 0} {\ frac {1} {t}} \ ln { \ frac {| \ delta \ mathbf {Z} (t) |} {| \ delta \ mathbf {Z} _ {0} |}}}$

A korlát biztosítja a lineáris közelítés érvényességét bármikor. ${\ displaystyle | \ delta \ mathbf {Z} _ {0} | \ to 0}$

Diszkrét időrendszer (térképek vagy fixpontos iterációk) esetén az ezzel kezdődő pálya a következőket jelenti: ${\ displaystyle x_ {n+1} = f (x_ {n})}$${\ displaystyle x_ {0}}$

${\ displaystyle \ lambda (x_ {0}) = \ lim _ {n \ to \ infty} {\ frac {1} {n}} \ sum _ {i = 0}^{n-1} \ ln | f '(x_ {i}) |}$

A Ljapunov -spektrum meghatározása

Egy dinamikus rendszerhez, amely evolúciós egyenlettel rendelkezik n -dimenziós fázistérben, a Ljapunov -spektrum ${\ displaystyle {\ dot {x}} _ {i} = f_ {i} (x)}$

${\ displaystyle \ {\ lambda _ {1}, \ lambda _ {2}, \ ldots, \ lambda _ {n} \} \ ,,}$

általában a kiindulási ponttól függ . Általában azonban egy dinamikus rendszer vonzóereje (vagy vonzói) iránt érdeklődünk , és általában minden egyes vonzóhoz egy kitevőkészlet tartozik. A kiindulási pont megválasztása meghatározhatja, hogy a rendszer melyik attraktoron végződik, ha több van. (A Hamilton -rendszerek esetében, amelyek nem rendelkeznek vonzókkal, ez nem aggodalomra ad okot.) A Ljapunov -kitevők leírják a vektorok viselkedését a fázistér érintőterében, és a jakobi mátrixból kerülnek meghatározásra.${\ displaystyle x_ {0}}$

${\ displaystyle J_ {ij} (t) = \ left. {\ frac {df_ {i} (x)} {dx_ {j}}} \ right | _ {x (t)}}$

ez a jakobiánus határozza meg az egyenleten keresztül a mátrix által megadott érintővektorok fejlődését${\ displaystyle Y}$

${\ displaystyle {\ dot {Y}} = JY}$

a kezdeti feltétellel . A mátrix leírja, hogyan terjed egy kis változás a ponton a végső pontra . A határ ${\ displaystyle Y_ {ij} (0) = \ delta _ {ij}}$${\ displaystyle Y}$${\ displaystyle x (0)}$${\ displaystyle x (t)}$

${\ displaystyle \ Lambda = \ lim _ {t \ rightarrow \ infty} {\ frac {1} {2t}} \ log (Y (t) Y^{T} (t))}$

mátrixot határoz meg (a határ meglétének feltételeit az Oseledets -tétel adja meg ). A Ljapunov -kitevőket a saját értékei határozzák meg . ${\ displaystyle \ Lambda}$${\ displaystyle \ lambda _ {i}}$${\ displaystyle \ Lambda}$

A Ljapunov -kitevők halmaza azonos lesz a dinamikus rendszer ergodikus összetevőjének szinte minden kiindulópontján .

Ljapunov kitevője az időben változó linearizációhoz

Hogy bevezessük Ljapunov exponens úgy alapvető mátrix (pl, a linearizálás mentén stacionárius megoldás egy folyamatos rendszerben, az alapvető mátrix , amely a lineárisan független megoldásokat az elsőrendű közelítése a rendszer. A szinguláris értékek a mátrix olyan a mátrix sajátértékeinek négyzetgyökei A legnagyobb Ljapunov -kitevő a következő ${\ displaystyle X (t)}$${\ displaystyle x_ {0}}$${\ displaystyle \ exp \ left (\ left. {\ frac {df^{t} (x)} {dx}} \ right | _ {x_ {0}} t \ right)}$${\ displaystyle \ {\ alpha _ {j} {\ big (} X (t) {\ big)} \} _ {1}^{n}}$${\ displaystyle X (t)}$${\ displaystyle X (t)^{*} X (t)}$${\ displaystyle \ lambda _ {\ mathrm {max}}}$

${\ displaystyle \ lambda _ {\ mathrm {max}} = \ max \ limits _ {j} \ limsup _ {t \ rightarrow \ infty} {\ frac {1} {t}} \ ln \ alpha _ {j} {\ nagy (} X (t) {\ nagy)}.}}$

AM Lyapunov bebizonyította, hogy ha az első közelítés rendszere rendszeres (pl. Minden állandó és periodikus együtthatójú rendszer szabályos), és legnagyobb Ljapunov -kitevője negatív, akkor az eredeti rendszer megoldása aszimptotikusan Lyapunov stabil . Később O. Perron kijelentette, hogy az első közelítés szabályszerűségének követelménye jelentős.

A legnagyobb Ljapunov -kitevőjel -inverzió Perron -hatásai

1930-ban O. Perron készített egy példát egy másodrendű rendszerre, ahol az első közelítés negatív Ljapunov-kitevővel rendelkezik az eredeti rendszer nulla megoldása mentén, de ugyanakkor az eredeti nemlineáris rendszer nulla megoldása Ljapunov instabil. Továbbá, ennek a nulla megoldásnak egy bizonyos környékén az eredeti rendszer szinte minden megoldásának pozitív Ljapunov -kitevője van. Ezenkívül lehetséges egy fordított példa létrehozása is, amelyben az első közelítésnek pozitív Lyapunov -kitevői vannak az eredeti rendszer nulla megoldása mentén, de ugyanakkor az eredeti nemlineáris rendszer nulla megoldása Lyapunov -stabil. Az eredeti rendszer és az első közelítés ugyanazon kiindulási adatokkal rendelkező megoldásainak Ljapunov előjeleinek inverziójának hatását később Perron -effektusnak neveztük.

Perron ellenpéldája azt mutatja, hogy a negatív legnagyobb Ljapunov -kitevő általában nem jelzi a stabilitást, és hogy a pozitív legnagyobb Ljapunov -kitevő általában nem jelzi a káoszt.

Ezért az időben változó linearizálás további indokolást igényel.

Alaptulajdonságok

Ha a rendszer konzervatív (azaz nincs disszipáció ), akkor a fázistér térfogat -eleme változatlan marad egy pálya mentén. Így az összes Ljapunov -kitevő összegének nullának kell lennie. Ha a rendszer disszipatív, a Ljapunov -kitevők összege negatív.

Ha a rendszer egy áramlás, és a pálya nem konvergál egyetlen pontba, akkor egy kitevő mindig nulla - a Ljapunov -kitevő az áramérték szerinti sajátvektorral rendelkező sajátértékének felel meg . ${\ displaystyle L}$

A Ljapunov -spektrum jelentősége

A Ljapunov -spektrum segítségével becsülhető az entrópiatermelés mértéke, a fraktál dimenzió és a vizsgált dinamikus rendszer Hausdorff -dimenziója . Különösen a Ljapunov-spektrum ismereteiből lehetséges az úgynevezett Ljapunov-dimenzió (vagy Kaplan – Yorke dimenzió ) megszerzése , amelyet a következőképpen határoznak meg: ${\ displaystyle D_ {KY}}$

${\ displaystyle D_ {KY} = k+\ sum _ {i = 1}^{k} {\ frac {\ lambda _ {i}} {| \ lambda _ {k+1} |}}}$

ahol a maximális egész szám, hogy a legnagyobb kitevők összege még mindig nem negatív. a rendszer információs dimenziójának felső határát jelenti . Ezenkívül az összes pozitív Lyapunov -kitevő összege Pesin -tételnek megfelelően megbecsüli a Kolmogorov – Sinai entrópiát . A Lyapunov-dimenzió becslésére és kiszámítására széles körben használt numerikus módszerek mellett létezik egy hatékony analitikai megközelítés, amely a közvetlen Ljapunov-módszerre épül, speciális Ljapunov-szerű funkciókkal. A korlátos pálya Ljapunov -kitevői és az attraktor Ljapunov -dimenziója változatlan a fázistér diffeomorfizmusa esetén. ${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle D_ {KY}}$

A legnagyobb Ljapunov -kitevő multiplikatív inverzét az irodalomban néha Ljapunov -időnek nevezik , és meghatározza a jellemző e -hajtogatási időt. A kaotikus pályákon a Ljapunov -idő véges, míg a rendszeres pályákon végtelen.

Numerikus számítás

Általában a Ljapunov -kitevők számítását a fentiek szerint nem lehet analitikusan elvégezni, és a legtöbb esetben numerikus technikákat kell igénybe venni. Egy korai példát, amely egyben a kaotikus pályák exponenciális divergenciájának első demonstrációját is jelentette, RH Miller készítette 1964 -ben. Jelenleg a leggyakrabban használt numerikus eljárás becsli a mátrixot a határmeghatározás több véges időközelítésének átlagolása alapján . ${\ displaystyle L}$${\ displaystyle L}$

Az egyik leggyakrabban használt és leghatékonyabb numerikus technika a Lyapunov -spektrum sima dinamikus rendszerhez történő kiszámításához a Lyapunov -vektorok periodikus Gram -Schmidt -ortonormalizálására támaszkodik, hogy elkerülje az összes vektor eltolódását a maximális tágulás irányában.

A Lyapunov -kitevők korlátozott kísérleti adatokból történő kiszámításához különböző módszereket javasoltak. Ezen módszerek alkalmazása azonban sok nehézséggel jár, és az ilyen problémákat óvatosan kell megközelíteni. A fő nehézség az, hogy az adatok nem tárják fel teljesen a fázisteret, inkább az attraktort korlátozzák, amely bizonyos irányok mentén nagyon korlátozott (ha van) kiterjesztéssel rendelkezik. Az adathalmazon belül ezek a vékonyabb vagy szingulárisabb irányok kapcsolódnak a negatívabb kitevőkhöz. A nemlineáris leképezések használata az attraktortól való kis elmozdulások fejlődésének modellezésére bizonyítottan jelentősen javítja a Ljapunov -spektrum helyreállításának képességét, feltéve, hogy az adatok nagyon alacsony zajszintűek. Az adatok szinguláris jellegét és a negatívabb kitevőkkel való kapcsolatát is feltárták.

Helyi Ljapunov -exponens

Míg a (globális) Ljapunov exponens mértékét adja meg a teljes kiszámíthatóság a rendszer, néha érdekes becsülni a helyi kiszámíthatóság egy pont körül x ₀ fázisban térben. Ez történhet a J ⁰ ( x ₀ ) jakobi mátrix sajátértékein keresztül . Ezeket a sajátértékeket helyi Ljapunov -kitevőknek is nevezik. (Figyelmeztetés: a globális kitevőkkel ellentétben ezek a helyi kitevők nem változatlanok a koordináták nemlineáris változása esetén).  

Feltételes Ljapunov -kitevő

Ezt a kifejezést általában a káosz szinkronizálására használják , amelyben két rendszer van összekapcsolva, általában egyirányú módon, úgy, hogy van meghajtó (vagy mester) rendszer és válasz (vagy szolga) rendszer. A feltételes kitevők azok a válaszrendszerek, amelyekben a hajtásrendszer egyszerűen (kaotikus) hajtásjel forrásaként van kezelve. A szinkronizálás akkor következik be, ha az összes feltételes kitevő negatív.

Lásd még

• Kaotikus keverés az alternatív levezetéshez
• Eden sejtése a Ljapunov -dimenzióról
• Floquet elmélet
• Liouville tétele (Hamilton -féle)
• Ljapunov dimenzió
• Ljapunov ideje
• Ismétlődés mennyiségi elemzése
• Oseledets -tétel

Hivatkozások

További irodalom

• Kuznyecov, Nyikolaj; Reitmann, Volker (2020). Vonzó dimenzióbecslések dinamikus rendszerekhez: elmélet és számítás . Cham: Springer.

• M.-F. Danca & NV Kuznyecov (2018). "Matlab kód a frakcionális rendszerű rendszerek Ljapunov-példányaihoz". International Journal of Bifurcation and Chaos . 25. cikk (5) bekezdés: art. szám 1850067. arXiv : 1804.01143 . doi : 10.1142/S0218127418500670 .

• Cvitanović P., Artuso R., Mainieri R., Tanner G. és Vattay G. Káosz: Klasszikus és Quantum Niels Bohr Intézet, Koppenhága 2005 - a káoszról szóló tankönyv a Free Documentation License alatt
• Freddy Christiansen és Hans Henrik Rugh (1997). "Ljapunov -spektrumok kiszámítása folyamatos Gram -Schmidt ortonormalizációval" . Nemlinearitás . 10 (5): 1063–1072. arXiv : chao-dyn/9611014 . Bibcode : 1997Nonli..10.1063C . doi : 10.1088/0951-7715/10/5/004 . S2CID  122976405 . 2006-04-25-én archiválva az eredetiből .

• Salman Habib és Robert D. Ryne (1995). "Ljapunov -exponensek szimplektikus számítása". Fizikai felülvizsgálati levelek . 74. (1): 70–73. arXiv : chao-dyn/9406010 . Bibcode : 1995PhRvL..74 ... 70H . doi : 10.1103/PhysRevLett.74.70 . PMID  10057701 . S2CID  19203665 .

• Govindan Rangarajan; Salman Habib és Robert D. Ryne (1998). "Ljapunov -exponensek átméretezés és újraértékelés nélkül". Fizikai felülvizsgálati levelek . 80 (17): 3747–3750. arXiv : chao-dyn/9803017 . Bibcode : 1998PhRvL..80.3747R . doi : 10.1103/PhysRevLett.80.3747 . S2CID  14483592 .

• X. Zeng; R. Eykholt és RA Pielke (1991). "A Ljapunov-exponens spektrum becslése alacsony pontosságú rövid idősorokból". Fizikai felülvizsgálati levelek . 66 (25): 3229–3232. Bibcode : 1991PhRvL..66.3229Z . doi : 10.1103/PhysRevLett.66.3229 . PMID  10043734 .

• E Aurell; G Boffetta; A Crisanti; G Paladin; A Vulpiani (1997). "Kiszámíthatóság nagyban: a Ljapunov -exponens fogalmának kiterjesztése". J. Phys. V: Math. Gen . 30. (1): 1–26. arXiv : chao-dyn/9606014 . Bibcode : 1997JPhA ... 30 .... 1A . doi : 10.1088/0305-4470/30/1/003 . S2CID  54697488 .

• F Ginelli; P Poggi; A Turchi; H Chaté; R Livi; A Politi (2007). "A dinamika jellemzése kovariáns Ljapunov -vektorokkal" (PDF) . Fizikai felülvizsgálati levelek . 99 (13): 130601. arXiv : 0706.0510 . Bibcode : 2007PhRvL..99m0601G . doi : 10.1103/PhysRevLett.99.130601 . hdl : 2158/253565 . PMID  17930570 . S2CID  21992110 . Archiválva az eredetiből (PDF) , 2008-10-31.

Szoftver

• [1] R. Hegger, H. Kantz és T. Schreiber, Nonlinear Time Series Analysis, TISEAN 3.0.1 (2007. március).
• [2] A Scientio ChaosKit terméke a Lyapunov -kitevőket számítja ki más kaotikus mérések mellett. A hozzáférés online elérhető egy webszolgáltatáson és a Silverlight demón keresztül.
• [3] Dr. Ronald Joe Record matematikai rekreációs szoftver laboratóriuma tartalmaz egy X11 grafikus klienst, a lyapot, amely grafikusan feltárja a kényszerített logisztikai térkép és más mértékegység -intervallumok térképeit. A mathrec szoftver laboratóriumának tartalma és kézikönyve szintén elérhető.
• [4] Az ezen az oldalon található szoftvereket kifejezetten a kitevők teljes spektrumának hatékony és pontos kiszámítására fejlesztették ki. Ez magában foglalja a LyapOde -ot olyan esetekben, amikor a mozgásegyenletek ismertek, valamint a Lyap -t olyan esetekben, amelyek kísérleti idősoros adatokat tartalmaznak. A LyapOde, amely "C" -ben írt forráskódot is tartalmaz, kiszámíthatja a feltételes Lyapunov -kitevőket a csatolt azonos rendszerekhez. Célja, hogy lehetővé tegye a felhasználó számára, hogy saját modell -egyenletkészletét adja meg, vagy használja a mellékelt egyenletek egyikét. A változók, paraméterek stb. Számának nincsenek korlátozásai. A Fortap -ban írt forráskódot tartalmazó Lyap kiszámíthatja a Ljapunov -irányvektorokat is, és jellemezheti a vonzó szingularitását, ami a fő oka a negatív kitevők az idősorok adataiból. Mindkét esetben kiterjedt dokumentáció és mintabeviteli fájlok találhatók. A szoftver lefordítható Windows, Mac vagy Linux/Unix rendszereken való futtatáshoz. A szoftver szöveges ablakban fut, és nem rendelkezik grafikus képességekkel, de olyan kimeneti fájlokat hozhat létre, amelyeket könnyen fel lehet rajzolni egy olyan programmal, mint az Excel.

Külső linkek

• Ljapunov kitevőjel -inverzióinak Perron -hatásai