Rod kalkulus - Rod calculus
Rod fogkő vagy rúd számításhoz a mechanikai módszer algoritmikus számítás számlálási rudak Kínában a hadviselő államok , hogy Ming-dinasztia , mielőtt a számlálási rudakat helyébe a sokkal kényelmesebb és gyorsabb Abacus . A rúdkalkulus kulcsfontosságú szerepet játszott a kínai matematika fejlődésében, egészen a Song-dinasztia és a Yuan-dinasztia magasságáig , amelynek csúcspontja Zhu Shijie munkájában legfeljebb négy ismeretlen polinomegyenlet feltalálása volt .

Hardver
A rúdszámítás elvégzésének alapfelszereltsége a számláló rudak és a számláló tábla köteg . A számláló rudak általában 12–15 cm hosszú, 2–4 mm átmérőjű bambuszrudakból készülnek, néha állatcsontokból, vagy elefántcsontból és jade-ból (jól sarkú kereskedők számára). A számláló tábla lehet asztallap, fatábla rácsral vagy anélkül, a padlón vagy a homokon.
1971-ben a kínai régészek egy jó állapotban megőrzött állatcsontszámláló botot tártak fel egy selyemzacskóban, amelyet a Han-dinasztia első felére (Kr. E. 206 - 8AD) származó Qian Yang megyében, Shanxi tartományban található sírból tároltak . 1975-ben egy köteg bambuszszámláló bot került elő.
Használata számláló rudak rúd fogkő virágzott a hadviselő államok , bár nem régészeti leletek találtak korábban, mint a nyugati Han-dinasztia (első felében Han-dinasztia , azonban a régészek nem felfedez szoftver utcafront rúd fogkő datálható Hadakozó Államok ); mivel a rúdszámítási szoftvernek biztosan együtt kellett működnie a rúdkalkulus hardverrel, nem kétséges, hogy a rúdkalkulus már több mint 2200 évvel ezelőtt a hadviselő államok idején virágzott.
Szoftver
A rúdszámításhoz szükséges legfontosabb szoftver egy Kínában az ókortól kezdve használt egyszerű, 45 mondatos helyzetbeli tizedes szorzótábla volt, az úgynevezett kilenc-kilenc tábla , amelyet tanulók, kereskedők, kormánytisztviselők és matematikusok egyaránt fejből megtanultak.
Rúdszámok
Számok megjelenítése
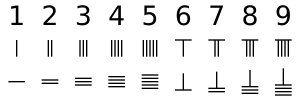
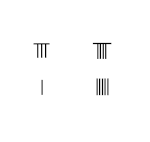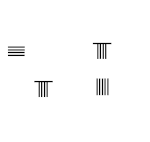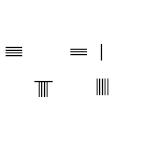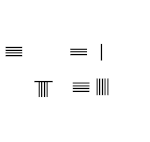
A rúdszámok az egyetlen numerikus rendszer, amely egyetlen szimbólum különböző elhelyezési kombinációit használja a tetszőleges szám vagy töredék átadására a tizedes rendszerben. A számok az egységek helyen, minden függőleges rúd képviseli 1. Két függőleges rudak képviselik 2, és így tovább, amíg 5 függőleges rudak, amely 5. szám 6 és 9 közötti, egy biquinary rendszert alkalmazunk, amelyben egy vízszintes rúd A függőleges sávok tetején az 5. szám látható. Az első sor az 1–9. szám rúdszámokkal, a második sor pedig vízszintes formában ugyanaz.
9-nél nagyobb számok esetén tizedesrendszert használnak. Az egységek helyétől balra elhelyezett rudak ennek a számnak a tízszeresét jelentik. A több száz helyre balra egy másik rudas készletet helyeznek el, amely ennek a számnak a 100-szorosát jelenti, és így tovább. Amint a szomszédos képen látható, a 231-es szám a rúdszámokkal van ábrázolva a felső sorban, az egyik rúd az egységek helyén az 1-et, a három rúd a tízes helyeken a 30-at, és két rúd a több száz helyen képviseli a 200-at, 231 összege.
A számítás során általában nem volt rács a felszínen. Ha a két, három és egy rúdszámot egymás után függőleges formában helyezzük el, akkor fennáll annak a lehetősége, hogy azt tévesen 51-re vagy 24-re tévesszük, amint az a szomszédos kép második és harmadik sorában látható. A félreértések elkerülése érdekében az egymást követő helyeken lévő számokat váltakozó függőleges és vízszintes formában helyezzük el, az egységeket függőleges formában, ahogy a jobb alsó sorban látható.
Nullák megjelenítése
A Rod számok , nulla képviseli a tér, ami egyszerre szolgál egy számot, és egy hely értéke. A hindu-arab számokkal ellentétben nincs külön szimbólum, amely a nullát jelöli. A szomszédos képen a nulla szám csupán szóközzel van ábrázolva.
Negatív és pozitív számok
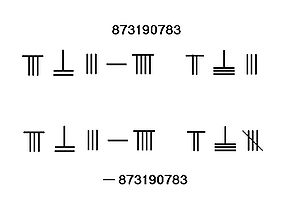
A dalmatematikusok a pirosat használták a pozitív számok, a feketét pedig a negatív számokat . Egy másik mód azonban az, hogy az utolsó helyre perjelet írunk, hogy megmutassuk, hogy a szám negatív.
Tizedes tört
Sunzi matematikai traktátusa decimális törtrészmetrológiát használt. A hosszegység 1 chi volt ,
1 chi = 10 cun , 1 cun = 10 fen , 1 fen = 10 li , 1 li = 10 hao , 10 hao = 1 shi, 1 shi = 10 hu .
1 chi 2 cun 3 fen 4 li 5 hao 6 shi 7 hu a mintaszámlára helyezzük
Qin Jiushao, a Southern Song dinasztia matematikusa kiterjesztette a tizedes tört használatát a metrológián túlra. Matematikai traktátum kilenc szakaszban című könyvében hivatalosan kifejezte 1,1446154 napját
Az egységet egy „日” (nap) szóval jelölte meg alatta.
Kiegészítés
A rúdkalkulus az összeadás elvén működik. Az arab számokkal ellentétben a számláló rudak által képviselt számjegyek additív tulajdonságokkal rendelkeznek. A hozzáadás folyamata a rudak mechanikus mozgatását jelenti, anélkül, hogy megjegyeznénk az összeadási táblázatot . Ez a legnagyobb különbség az arab számokhoz képest, mivel nem lehet mechanikusan összerakni az 1-et és a 2-t a 3-ra, vagy a 2-et és a 3-t az 5-ös formára.
A szomszédos kép bemutatja a 3748 és 289 hozzáadásának lépéseit:
- Helyezze a 3748 rugót az első sorba, a másodikba pedig a 289-et.
- Számítson balról jobbra, először a 2/289-ből.
- Vegyen el két rudat alulról, és adjon 7-et a tetejére, hogy 9 legyen.
- Mozgasson 2 rudat fentről lefelé 8, vigye az egyiket előre a 9-re, amely nulla lesz és 3-ra viszi a 4-et, a 8-at távolítsa el az alsó sorból.
- Helyezzen egy rudat a felső sor 8-ról az alsó 9-re, hogy kialakítson egy hordozót a következő rangra, és adjon hozzá egy rudat a felső sor 2 rudához, hogy 3 rudat készítsen, a felső sor bal 7.
- Eredmény 3748 + 289 = 4037
Az emelő rúdjai az adagolás során változnak, míg az alul lévő rúd rudai "eltűnnek".
Kivonás
Hitelfelvétel nélkül
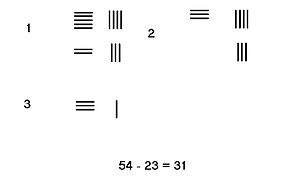
Abban a helyzetben, amikor nincs szükség hitelfelvételre , csak az almenetről kell a rudak számát levenni a minuendából . A számítás eredménye a különbség. A szomszédos képen láthatjuk a 23 kivonásának lépéseit 54-ből.
Hitelfelvétel
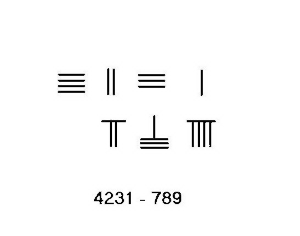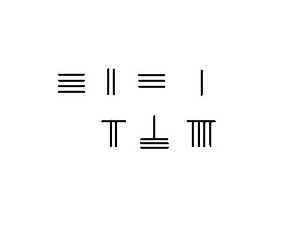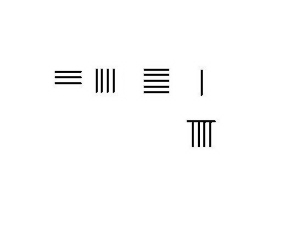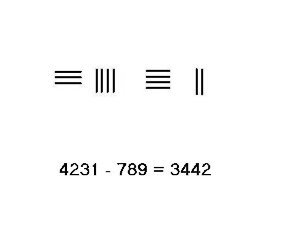
Olyan helyzetekben, amikor hitelfelvételre van szükség, például 4231–789, bonyolultabb eljárást kell alkalmazni. Ennek a példának a lépései a bal oldalon láthatók.
- Helyezze a 4231 minuendet a tetejére, az aljára pedig a 789-et. Számoljon balról jobbra.
- Kölcsönözzön egyet az ezer helyről tízesért a több száz helyen, mínusz 7-vel az alábbi sorból, a 3-as különbséget hozzáadjuk a tetején lévő 2-hez, hogy kialakuljon az 5. Az alul levő 7-et kivonjuk, amit a szóköz mutat.
- Kölcsönözzön 1-et a több száz helyről, amiből a 4. A tízes helyen levő 10 mínusz az alábbi 8 eredményez 2-t, ami hozzáadódik a fenti 3-hoz, így az 5. képződik. A felső sor most 3451, az alsó 9.
- Kölcsönözzön egyet az 5-ből a tetején lévő tízes helyen, amiből 4 marad. A tízesből kölcsönvett 1 az egység helyén 10, levonva 9-et, ami 1-et eredményez, amelyet a tetejére adunk, hogy kialakuljon 2. az alsó sor kivonva, a felső sorban szereplő 3442 ekkor a számítás eredménye
Szorzás
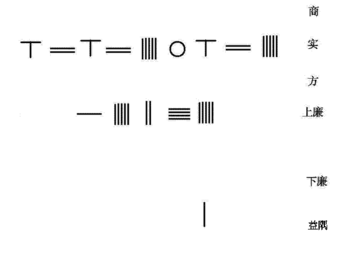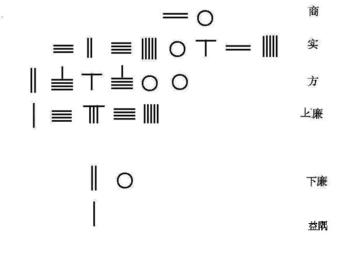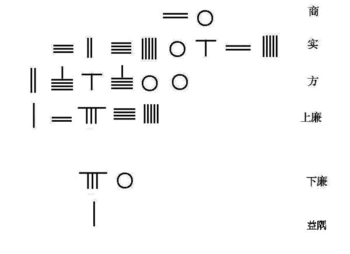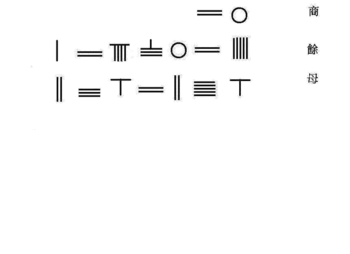
Sunzi Suanjing részletesen leírta a szorzás algoritmusát. A bal oldalon láthatók a 38 × 76 kiszámításához szükséges lépések:
- Helyezze a szorzót felülre, a szorzót alulra. Sorolja fel a szorzó egységeinek helyét a szorzó legmagasabb helyével. Hagyjon középen helyet a felvételhez.
- Kezdje el a számítást a multiplandum legmagasabb helyéről (a példában számoljon 30 × 76, majd 8 × 76). A szorzótábla használatával 3-szor 7 a 21. Helyezzen 21-et rudakba középen, az egyiket igazítsa a szorzó tízes helyéhez (7 tetején). Ezután háromszor 6 egyenlő 18-val, helyezze a 18-at a képen látható módon. Ha a multiplikandumban lévő 3-at teljesen megszorozzuk, vegyük le a rudakat.
- Mozgassa a szorzót egy hellyel jobbra. Változtassa 7-et vízszintesre, 6-t függőlegesre.
- 8 × 7 = 56, helyezze az 56-ot a középső második sorba úgy, hogy a helyegységek a szorzóban megszorzott számjegyekkel igazodjanak. Vegyen ki 7-et a szorzóból, mivel megsokszorozták.
- 8 × 6 = 48, az utolsó lépés hatosához hozzáadva 4-et 10-re, 1-et viszünk át. Vegye le az egységek közül 8-at a multiplikátorban, és vegyen le 6-at a szorzó egységeinek helyéről.
- Összegezze a 2380-at és az 508-at középen, aminek eredményeként 2888: a szorzat.
Osztály
.
A bal oldali animáció a számítás lépéseit mutatja 309/7 = 441/7.
- Helyezze a 309 osztalékot a középső sorba, a 7-es osztót az alsó sorba. Hagyjon helyet a felső sornak.
- Mozgassa a 7-es osztót egy hellyel balra, vízszintesre változtatva.
- A kínai szorzótábla és osztás használatával a 30 ÷ 7 egyenlő 4 maradékkal. Helyezze a 4 hányadost a felső sorba, a maradékot pedig 2 a középső sorba.
- Mozgassa az osztót egy hellyel jobbra, függőlegesre változtatva. 29 ÷ 7 egyenlő 4 maradék 1. Helyezze a 4-es hányadost a tetejére, az osztót a helyén hagyva. Helyezze a maradékot a középső sorba az osztalék helyett ebben a lépésben. Az eredmény az, hogy a hányados 44, a maradék pedig 1
Al Khwarizmi a szétválás Sunzi algoritmusát indiai forrásokból 825-ben indiai forrásokból toto útján továbbította az iszlám országnak. Al Khwarizmi könyvét a 13. században fordították latinra, a Sunzi-osztási algoritmus később Galley-divízióvá fejlődött Európában. A szétválás algoritmus Abu'l-Hasan al-Uqlidisi 's 925AD könyv Kitab al-Fusul fi al-Hisab al-Hindi és a 11. században Kushyar ibn Labban ' s Principles of Reckoning hindu azonosak voltak Sunzu részlege algoritmus.
Törtek
Ha van egy maradék egy helyérték decimális rúd számítási osztásában, akkor a maradékot és az osztót is a helyén kell hagyni úgy, hogy egyik a másikra kerüljön. A Liu Hui „s megjegyzések Jiuzhang suanshu (2. század BCE), a szám a tetején az úgynevezett "shi"(实), míg az egy alul az úgynevezett "fa"(法). A Sunzi Suanjingben a tetején lévő számot "zi" (子) vagy "fenzi" (lit., frakció fia), az alján levő számot "mu" (母) vagy "fenmu" (lit. , a frakció anyja). A Fenzi és a Fenmu a modern kínai név a számlálónak és a nevezőnek is . Amint a jobb oldalon látható, 1 a maradék számláló, 7 a nevező osztó, amely egy törtet alkot1/7. Az osztás hányadosa309/7 értéke 44 + 1/7. Liu Hui sok töredékes számítást alkalmazott Haidao Suanjing-ben .
Ezt a frakciót, amelynek tetején számláló, alján pedig nevező található, vízszintes sáv nélkül, az al Khwarizmi Indián keresztül 825AD könyvében továbbította arab országba , és a 10. század Abu'l-Hasan al-Uqlidisi és a 15. századi Jamshīd al-Kāshī "Aritematikus kulcs" című műve.
Kiegészítés
1/3 + 2/5.
- Helyezze a két számlálót 1 és 2 a számláló tábla bal oldalára, a két nevezőt 3 és 5 a jobb oldalra
- Kereszt szorozzon 1-et 5-tel, 2-t 3-mal, hogy 5-öt és 6-ot kapjon, cserélje ki a számlálókat a megfelelő kereszttermékekre.
- Szorozza meg a két nevezőt 3 × 5 = 15, tegye a jobb alsó sarokba
- Adja hozzá a számlálótábla jobb felső sarkába helyezett két számlálót: 5 és 6 = 11.
- Eredmény: 1/3 + 2/5. = 11./15
Kivonás
8./9. - 1/5.
- Tegye le az 1. és 8. számláló rúdszámát a számláló tábla bal oldalán
- Tegye le az 5. és 9. nevező rudait a számláló tábla jobb oldalán
- Kereszt szorzás 1 × 9 = 9, 5 × 8 = 40, cserélje ki a megfelelő számlálókat
- Szorozzuk meg az 5 × 9 = 45 nevezőket, tegyünk 45-et a számlálótábla jobb alsó sarkába, cseréljük le az 5 nevezőt
- Vonj le 40 - 9 = 31, tedd a jobb felsőbe.
- Eredmény: 8./9. - 1/5. = 31/45
Szorzás
31/3 × 52/5.
- Rendezze a számláló rudakat 3-ra1/3 és 52/5. a számláló táblán shang, shi, fa táblázatos formátumban.
- shang-szor fa hozzá a shihez: 3 × 3 + 1 = 10; 5 × 5 + 2 = 27
- shi szorozva shi-vel: 10 × 27 = 270
- fa szorozva fa: 3 × 5 = 15
- shi osztva fa-val: 31/3 × 52/5. = 18
Legnagyobb közös tényező és frakciócsökkentés
A két szám közül a legmagasabb közös tényező megállapítására és a frakció csökkentésére vonatkozó algoritmust Jiuzhang suanshu írta le . A legmagasabb közös tényezőt a maradékokkal való egymás utáni osztás találja meg, amíg az utolsó két maradék meg nem egyezik. A jobb oldali animáció szemlélteti a legmagasabb közös tényező megtalálásának algoritmusát32,450,625/59 056 400 és egy frakció csökkentése.
Ebben az esetben a hcf értéke 25.
Osszuk el a számlálót és a nevezőt 25-tel. A csökkentett frakció az1,298,025/2,362,256.
Interpoláció
Calendarist és matematikus Ő Chengtian (何承天) használt frakció interpolációs módszer, az úgynevezett „harmonizálása az osztó a nap” (调日法), így jobban közelítő érték, mint a régi fokozatos közelítéssel hozzáadjuk a számláló és nevező a „gyengébb” frakció "erősebb frakcióval". Zu Chongzhi legendás π =355/113 He Chengtian módszerével megszerezhető volt
Lineáris egyenletrendszer
Nyolcadik fejezet Négyszögletű tömbje Jiuzhang suanshu előírt algoritmus megoldása a lineáris egyenletek szerint eljárás megszüntetése :
8-1. Feladat: Tegyük fel, hogy 3 csomag kiváló minőségű gabonafélék, 2 köteg közepes minőségű gabonafélék és egy köteg alacsony minőségű gabonafélék vannak gyűjtve 39 dou tömeggel. Van még 2, 3 és 1 kötegük a megfelelő gabonafélékből, amelyek összege 34 dou; 1,2 és 3 köteg gabonafélénk is van, összesen 26 dou.
Keresse meg a felső, közepes és rossz minőségű gabonafélék mennyiségét. Az algebrában ezt a problémát három rendszeregyenlettel fejezhetjük ki, három ismeretlenrel.
Ezt a problémát Jiuzhang suanshu- ban oldották meg egy számlálótáblán 3x4-es mátrixhoz hasonló táblázatos formában elhelyezett számláló rudakkal:
| minőség | bal oszlop | középső oszlop | jobb oldali oszlop |
| tetejére |
|
|
|
| közepes |
|
|
|
| alacsony |
|
|
|
| shi |
|
|
|
Algoritmus:
- Szorozza meg a középső oszlopot a jobb oszlop csúcsminőségű számával.
- Ismételten vonja le a jobb oldali oszlopot a középső oszlopból, amíg a középső oszlop felső száma = 0
- szorozza meg a bal oszlopot a jobb oszlop felső sorának értékével
- Ismételten vonja ki a jobb oldali oszlopot a bal oszlopból, amíg a bal oszlop felső száma = 0
- Miután a fenti eliminációs algoritmust alkalmaztuk a redukált középső oszlopra és a bal oszlopra, a mátrixot háromszög alakúra redukáltuk:
| minőség | bal oszlop | középső oszlop | jobb oldali oszlop |
| tetejére |
|
||
| közepes |
|
|
|
| alacsony |
|
|
|
| shi |
|
|
|
Az alacsony minőségű gabona mennyisége a kötegben =
Ebből könnyen megtalálható egy köteg felső és közepes minőségű gabona mennyisége:
Egy csomag kiváló minőségű gabona = 9 dou
Egy köteg közepes gabonafélék = 4 dou >
A négyzetgyök kivonása
A négyzetgyök kinyerésének algoritmusát a Jiuzhang suanshu , Sunzi Suanjing szakirodalomban pedig kisebb terminológiai különbségekkel írták le .
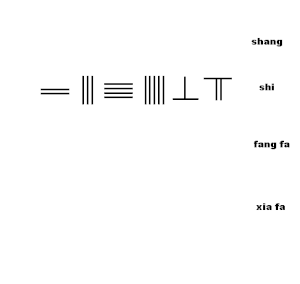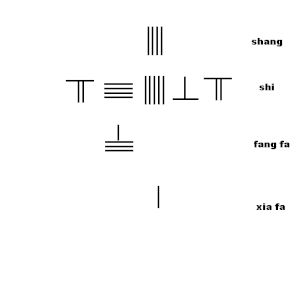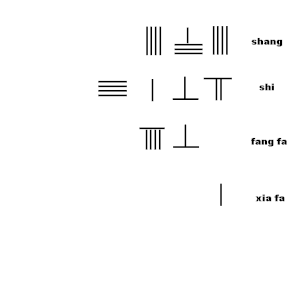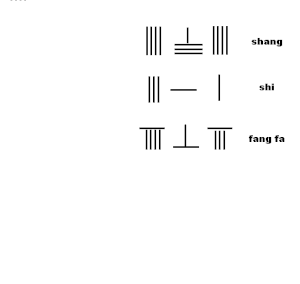
Az animáció a négyzetgyök közelítésének rúdszámítási módszerrel történő kinyerésének algoritmusát mutatja be az algoritmusból a Sunzi Suanjing 19. fejezetének 2. fejezetében:
- Most van egy négyzet alakú terület 234567, keresse meg a tér egyik oldalát .
Az algoritmus a következő:
- Állítsa be a 234567-et a számláló táblán, felülről a második sorban, shi néven
- Állítson be 1-es jelölőt 10000-as helyzetben a 4. sorban, xia fa néven
- Becsülje meg a négyzetgyök első számjegyét, amely a 4-es rúdszámot számolja, tegye a felső sor ( shang ) százas pozíciójára,
- Szorozza meg a shang 4-et xiafa 1-gyel, tegye a 4-es terméket a fang fa nevű 3. sorba
- Szorozzuk meg a shang- ot agyarral fa vonjuk le a 4x4 = 16 szorzót a shi-ből : 23-16 = 7, maradjunk 7-es szám.
- duplázza meg az agyag fa 4-et, hogy 8 legyen, egy pozíciót toljon jobbra, és a függőleges 8-t vízszintesre változtassa 8-ra, miután jobbra mozgatta.
- Mozgassa xia fa két pozíciót jobbra.
- Becsülje meg a shang második számjegyét 8-ra: tegye a 8. számot a felső sor tizedik pozíciójába.
- Szorozzuk meg xia fa- t a shang új számjeggyel , adjuk hozzá a fang fa-t
.
- 8 hívás 8 = 64, vonja le a 64-et a felső sor "74" számáról, így egy rúd marad a legjelentősebb számjegynél.
- duplázza meg a fang fa 8 utolsó számjegyét , adja hozzá a 80 = 96 értéket
- Mozgassa a fang fa 96-ot egy pozícióval jobbra, változtasson a konvención; mozgassa xia fa "1" két pozíciót jobbra.
- Becsülje meg a shang 3. számjegyét 4-re.
- Szorozza meg a 4-es shang új számjegyét a xia fa 1-gyel, és az agy-fa- val kombinálva 964-et.
- vonja le egymástól 4 * 9 = 36,4 * 6 = 24,4 * 4 = 16 a shi-ből , így 311 marad
- duplázza meg a fang fa utolsó 4 számjegyét 8-ba, és olvassa el az fang fa-t
- eredmény
Jia Xian , az Észak-Song dinasztia matematikusa kifejlesztett egy additív multiplikatív algoritmust a négyzetgyök kinyerésére , amelyben a "fang fa" hagyományos "duplázását" helyettesítette azzal, hogy a shang számot a fang fa számjegyhez adta , ugyanazzal a hatással.
Köbös gyökér kivonása
Jiuzhang suanshu vol iv "shaoguang" algoritmust adott a köbös gyökér kivonására.
一九〕 今 有 積 一百 八十 六萬 八百 六十 七尺。 問 為 立方 幾何? 答曰 : 一百 二十 三尺。。
19. probléma: Van egy 1860867 köbös chi, mekkora az oldal hossza? Válasz: 123 chi.
Jia Xian, az Észak-Song dinasztia matematikusa a Horner-séma egyszerűsített formájához hasonló módszert talált ki a köbgyök kinyerésére. A jobb oldali animáció Jia Xian algoritmusát mutatja be a 19. feladat megoldására a Jiuzhang suanshu 4. kötetben.
Polinomiális egyenlet
Az Észak-Song dinasztia matematikusa, Jia Xian kitalálta a Horner-sémát a forma egyszerű 4. rendű egyenletének megoldására
Qin Jiushao, a South Song-dinasztia matematikusa javította Jia Xian Horner-módszerét, hogy megoldja a polinomegyenletet a 10. sorrendig. A következő algoritmus a megoldásra
- az ő matematikai Értekezés a kilenc szakasz 6. kötet probléma 2.
Ezt az egyenletet alulról felfelé rendeztük, számláló rudakkal, a számláló táblán táblázatos formában
| 0 | shang | gyökér |
| 626250625 | shi | állandó |
| 0 | agyar | x együttható |
| 15245 | shang lian | x ^ 2 pozitív együtthatója |
| 0 | fu lian | x ^ 2 negatív együtthatója |
| 0 | xia lian | x ^ 3 koefe |
| 1 | yi yu | X ^ 4 negatív együtthatója |
Algoritmus:
- Rendezze el az együtthatókat táblázatos formában, állandó a shi-nél, az x koeffienctje a shang lian-nál, az X ^ 4 coeffiecntje pedig yi yu-nál; igazítsa a számokat egység rangra.
- Előzetes shang lian két rangot
- Haladj előre három sorban
- Becsülje meg a shang = 20 értéket
- legyen xia lian = shang * yi yu
- legyen fu lian = shang * yi yu
- fu lian és shang lian egyesítése
- hagyja agyar = shang * shang lian
- vonja le a shi * agyarát
- add shang * yi yu-t xia lian-hoz
- visszahúzza xia lian 3 rangot, visszahúzza yi yu 4 rangot
- A shang második számjegye 0
- egyesíti a shang lian-t agyarrá
- egyesítsd yi yu-t xia lian-ba
- Adja hozzá yi yu-t a fu lianhoz, vonja le az eredményt a agyarról, legyen az eredmény nevezője
- keresse meg a legmagasabb közös tényezőt = 25, és egyszerűsíti a törtet
- megoldás
Tian Yuan shu

Li Zhi jüan dinasztia matematikus Tian jüan shu-val fejlesztette ki a rúdkalkulációt
Példa Li Zhi Ceyuan haijing II. Kötet, egy ismeretlen 14. feladategyenlete:
Négy ismeretlen polinomiális egyenlete
Zhu Shijie matematikus tovább fejlesztette a rúdkalkulációt, hogy 2–4 ismeretlen polinomiális egyenletet tartalmazzon.
Például három ismeretlen polinomjai:
1. egyenlet:
2. egyenlet:
3. egyenlet:
Két ismeretlen egymást követő megszüntetése után három ismeretlen polinomiális egyenleteit egy ismeretlen polinomiális egyenletévé redukálták:
Megoldva x = 5;
Lásd még
Hivatkozások
- Lam Lay Yong (蓝 丽蓉) Ang Tian Se (洪 天赐), Fleeting Footpseps, World Scientific ISBN 981-02-3696-4
- Jean Claude Martzloff, A kínai matematika története ISBN 978-3-540-33782-9



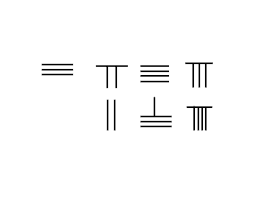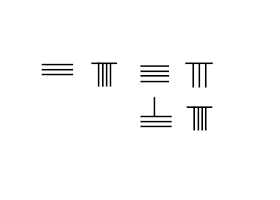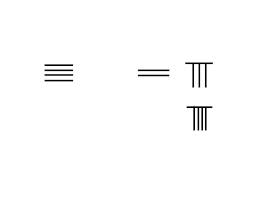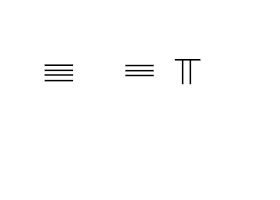






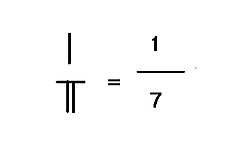











![\ sqrt [3] (1860867) = 123](https://wikimedia.org/api/rest_v1/media/math/render/svg/1446541cf1cd6c1d0866f8e017ef6f5280f1f415)