Monoton funkció - Monotonic function

1. ábra. Monoton nem csökkenő függvény.

2. ábra. Monoton nem növekvő függvény

3. ábra: Nem monoton függvény

A matematikában a monoton függvény (vagy monoton függvény ) a rendezett halmazok közötti függvény, amely megőrzi vagy megfordítja az adott sorrendet . Ez a koncepció ben merült fel , számolás , később általánossá az elvontabb beállítását rendezett halmaz .

Számításban és elemzésben

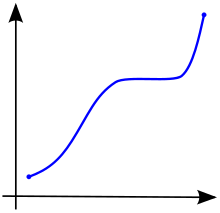
A számításban a valós számok egy részhalmazán meghatározott függvényt valós értékekkel akkor és csak akkor nevezzük monotonnak, ha vagy teljesen nem növekvő, vagy teljesen nem csökkenő. Vagyis az 1. ábra szerint a monoton növekvő függvénynek nem kell kizárólag növekednie, egyszerűen nem szabad csökkennie. ${\ displaystyle f}$

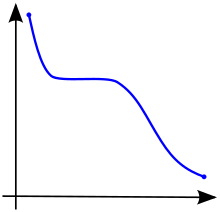
Egy függvény nevezzük monoton nő (szintén növekvő vagy nem csökkenő ), ha minden , és olyan, hogy az egyik, , így megőrzi a sorrendben (lásd 1. ábra). Hasonlóképpen, egy függvényt monoton csökkenőnek ( csökkenőnek vagy nem növekvőnek) is neveznek, ha, amikor , akkor , tehát megfordítja a sorrendet (lásd 2. ábra). ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle x \ leq y}$${\ displaystyle f \! \ left (x \ right) \ leq f \! \ left (y \ right)}$${\ displaystyle f}$${\ displaystyle x \ leq y}$${\ displaystyle f \! \ left (x \ right) \ geq f \! \ left (y \ right)}$

Ha a monotonitás definíciójában a sorrendet a szigorú rend váltja fel , akkor az ember erősebb követelményt kap. Az ezzel a tulajdonsággal rendelkező függvényt szigorúan növekvőnek (szintén növekvőnek ) nevezzük . Ismét a sorrend szimbólumának megfordításával találunk egy megfelelő fogalmat, amelyet szigorúan csökkenőnek (szintén csökkenőnek ) neveznek . Egy függvényt szigorúan monotonnak nevezhetünk, ha szigorúan növekszik vagy szigorúan csökken. Funkciók, amelyek szigorúan monoton van egy-egy (mert nem egyenlő , vagy vagy és így, a monotonitás, akár vagy , így .) ${\ displaystyle \ leq}$${\ displaystyle <}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle x <y}$${\ displaystyle x> y}$${\ displaystyle f \! \ left (x \ right) <f \! \ left (y \ right)}$${\ displaystyle f \! \ left (x \ right)> f \! \ left (y \ right)}$${\ displaystyle f \! \ left (x \ right) \ neq f \! \ left (y \ right)}$

Ha nem világos, hogy a "növekvő" és a "csökkenő" magában foglalja annak lehetőségét, hogy ugyanazt az értéket egymás utáni érveken ismételjük meg, akkor a gyengén monoton , gyengén növekvő és gyengén csökkenő kifejezéseket használhatjuk ennek a lehetőségnek a hangsúlyozására.

A "nem csökkenő" és a "nem növekvő" kifejezéseket nem szabad összetéveszteni a "nem csökkenő" és a "nem növekvő" (sokkal gyengébb) negatív minősítésekkel. Például a 3. ábra függvénye először leesik, majd felemelkedik, majd ismét leesik. Ezért nem csökken és nem növekszik, de nem nem csökken, és nem növekszik.

A funkció azt mondják, hogy teljesen monoton Egy intervallumon , ha az származékok összes rend van nemnegatív vagy az összes nem pozitív minden pontján az intervallumon. ${\ displaystyle f \! \ left (x \ right)}$${\ displaystyle \ left (a, b \ right)}$${\ displaystyle f}$

A funkció fordítottja

Egy függvénynek, amely monoton, de nem szigorúan monoton, és így állandó egy intervallumon, nincs fordítottja. Ennek az az oka, hogy ahhoz, hogy egy függvény inverz legyen, szükség van egy-egy leképezésre a tartománytól a függvény tartományáig. Mivel a monoton függvénynek vannak bizonyos értékei, amelyek állandóak a tartományában, ez azt jelenti, hogy egynél több érték lenne a tartományban, amely ezt az állandó értéket képezi le.

Azonban egy y = g ( x ) függvénynek , amely szigorúan monoton, van egy fordított függvénye, így x = h ( y ), mert garantáltan mindig egy-egy leképezés lesz a függvény tartományától a tartományig. Ezenkívül egy függvény egy értéktartományban szigorúan monotonnak mondható, és így fordított értékkel rendelkezik. Például, ha y = g ( x ) szigorúan monoton az [ a , b ] tartományban , akkor fordított x = h ( y ) van a [ g ( a ), g ( b )] tartományban, de nem mondhatjuk, hogy a függvény teljes tartománya fordított.

Megjegyzendő, hogy néhány tankönyv tévesen azt állítja, hogy a monoton függvényhez inverz létezik, amikor valójában azt jelenti, hogy a szigorúan monoton függvényhez fordított létezik.

Monoton átalakulás

A monoton transzformáció (vagy monoton transzformáció ) kifejezés is okozhat némi zavart, mert egy szigorúan növekvő függvényből származó transzformációra utal. Ez a helyzet a közgazdaságtanban, ha a hasznossági függvény sorrendi tulajdonságait a monoton transzformáció során megőrzik (lásd még a monoton preferenciákat ). Ebben az összefüggésben az, amit "monoton transzformációnak" nevezünk, pontosabban "pozitív monoton transzformációnak" nevezzük, hogy megkülönböztessük azt a "negatív monoton transzformációtól", amely megfordítja a számok sorrendjét.

Néhány alapvető alkalmazás és eredmény

A következő tulajdonságok igazak egy monoton funkcióra : ${\ displaystyle f \ colon \ mathbb {R} \ to \ mathbb {R}}$

• ${\ displaystyle f}$van korlátai a jobb és a bal oldalon minden pontján a domén ;
• ${\ displaystyle f}$határa van a pozitív vagy negatív végtelennél ( ) vagy valós szám , vagy .${\ displaystyle \ pm \ infty}$${\ displaystyle \ infty}$${\ displaystyle -\ infty}$
• ${\ displaystyle f}$csak ugrásmegszakítások lehetnek ;
• ${\ displaystyle f}$Egyszerre csak megszámlálható sok folytonossági saját domain. A diszkontinuitások azonban nem feltétlenül állnak izolált pontokból, sőt akár sűrűek is lehetnek az ( a , b ) intervallumban .

Ezek a tulajdonságok az oka annak, hogy a monoton függvények hasznosak az elemzés technikai munkájában . Néhány további tény ezekről a funkciókról:

• ha egy monoton függvény egy intervallumon , akkor az differenciálható szinte mindenütt az ; vagyis a számok halmaza az , hogy nem differenciálható olyan Lebesgue intézkedés nulla . Ezenkívül ez az eredmény nem javítható számlálhatóvá: lásd Cantor függvény .${\ displaystyle f}$ ${\ displaystyle I}$${\ displaystyle f}$ ${\ displaystyle I}$${\ displaystyle x}$${\ displaystyle I}$${\ displaystyle f}$${\ displaystyle x}$
• ha ez a halmaz számolható, akkor abszolút folyamatos.${\ displaystyle f}$
• ha egy monoton függvény intervallumon , akkor a Riemann integrálható .${\ displaystyle f}$${\ displaystyle \ left [a, b \ right]}$${\ displaystyle f}$

A monoton függvények fontos alkalmazása a valószínűségelmélet . Ha egy véletlen változó , akkor annak kumulatív eloszlásfüggvénye monoton növekvő függvény. ${\ displaystyle X}$ ${\ displaystyle F_ {X} \! \ left (x \ right) = {\ text {Prob}} \! \ left (X \ leq x \ right)}$

Egy függvény akkor unimodális, ha egy bizonyos pontig ( mód ) monoton növekszik, majd monoton csökken.

Amikor egy szigorúan monoton függvény, akkor az injektív a saját domain, és ha a tartomány az , akkor van egy inverz függvény a számára . Ezzel szemben minden állandó függvény monoton, de nem injektív, és ezért nem lehet inverz. ${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle T}$${\ displaystyle f}$${\ displaystyle T}$${\ displaystyle f}$

Topológiában

Egy térkép monotonnak mondható, ha minden szála össze van kötve; azaz, minden egyes eleme a (esetleg üres) halmaz van csatlakoztatva. ${\ displaystyle f: X \ rightarrow Y}$${\ displaystyle y}$${\ displaystyle Y}$${\ displaystyle f^{-1} (y)}$

Funkcionális elemzésben

A funkcionális elemzés a topológiai vektor teret , egy (esetleg nem-lineáris) operátor azt mondják, hogy egy monoton üzemeltető , ha ${\ displaystyle X}$${\ displaystyle T: X \ rightarrow X^{*}}$

${\ displaystyle (Tu-Tv, uv) \ geq 0 \ quad \ forall u, v \ in X.}$

Kachurovskii tétele azt mutatja, hogy a Banach -terek konvex függvényeinek monoton operátorai származnak.

A betegek egy részénél az azt mondta, hogy egy monoton halmaz , ha minden párt és az , ${\ displaystyle G}$${\ displaystyle X \ x X^{*}}$${\ displaystyle [u_ {1}, w_ {1}]}$${\ displaystyle [u_ {2}, w_ {2}]}$${\ displaystyle G}$

${\ displaystyle (w_ {1} -w_ {2}, u_ {1} -u_ {2}) \ geq 0.}$

${\ displaystyle G}$akkor mondható maximális monotonnak, ha az összes monoton halmaz között maximális a halmazbefogadás értelmében. A monoton operátor grafikonja monoton halmaz. A monoton operátort akkor nevezzük maximális monotonnak, ha a grafikonja a maximális monoton halmaz . ${\ displaystyle G (T)}$

A rendelméletben

A rendelmélet a valós számok általánosításaként az önkényes részben rendezett halmazokkal és az előre megrendelt halmazokkal foglalkozik . A monotonitás fenti definíciója ezekben az esetekben is releváns. A „növekvő” és „csökkenő” kifejezéseket azonban kerüljük, mivel hagyományos képi megjelenítésük nem vonatkozik a nem teljes megrendelésekre . Ezenkívül a szigorú kapcsolatoknak <és> kevés haszna van sok nem teljes megrendelésben, ezért nem vezetnek be hozzájuk további terminológiát.

Ha hagyjuk , hogy ≤ bármely részlegesen rendezett halmaz részleges sorrendi viszonyát jelöli, a monoton függvény, más néven izotónus , vagy rendfenntartó , kielégíti az ingatlant

x ≤ y azt jelenti, hogy f ( x ) ≤ f ( y ),

minden x és y számára a tartományában. A két monoton leképezés összetett eleme is egyhangú.

A kettős fogalma gyakran nevezik antitone , anti-monoton , vagy annak érdekében, irányváltó . Ennélfogva az f antitone függvény kielégíti a tulajdonságot

x ≤ y azt jelenti, hogy f ( y ) ≤ f ( x ),

minden x és y számára a tartományában.

Egy konstans függvényt egyszerre monoton és antitone; Ezzel szemben, ha f egyszerre monoton és antitone, és ha a domain f egy rács , akkor f állandónak kell lennie.

A monoton függvények a sorrendelmélet központi elemei. A témával foglalkozó cikkek többségében megjelennek, és speciális alkalmazások példái találhatók ezeken a helyeken. Néhány figyelemre méltó speciális monoton függvény a sorrendbeágyazás (olyan függvény, amelyhez x ≤ y csak akkor és csak akkor, ha f ( x ) ≤ f ( y )) és a sorrendi izomorfizmus ( szurjektív sorrend beágyazása).

A keresési algoritmusok összefüggésében

A keresési algoritmusok összefüggésében a monotonitás (más néven konzisztencia) a heurisztikus függvényekre alkalmazott feltétel . A heurisztikus h (n) monoton, ha minden csomópont n , és minden utódja n „ az n által generált minden olyan intézkedés egy , a becsült költsége eléri a célt n nem nagyobb, mint a lépés költsége egyre n” , valamint a a cél elérésének becsült költsége n -ből ,

${\ displaystyle h (n) \ leq c \ left (n, a, n '\ right)+h \ left (n' \ right).}$

Ez a háromszög -egyenlőtlenség egyik formája , n , n ' , és a _n célhoz legközelebb eső G n . Mivel minden monoton heurisztika is elfogadható , a monotonitás szigorúbb követelmény, mint az elfogadhatóság. Néhány heurisztikus algoritmus, például az A* , optimálisnak bizonyítható, feltéve, hogy az általuk használt heurisztika monoton.

Logikai függvényekben

A nemmonoton függvénnyel "ha a, akkor mind b, mind c " hamis csomópontok jelennek meg a valódi csomópontok felett .

A "legalább kettő a , b , c tartásból" monoton függvény Hasse diagramja . A színek a funkció kimeneti értékeit jelzik.

A Boole -algebrában a monoton függvény olyan, hogy a {0,1} összes a _i és b _i esetében, ha a ₁ ≤ b ₁ , a ₂ ≤ b ₂ , ..., a _n ≤ b _n (azaz Descartes-szorzat {0, 1} ⁿ rendelik coordinatewise ), majd f ( a ₁ , ..., a _n ) ≤ f ( b ₁ , ..., b _n ) . Más szóval, a Boole -függvény monoton, ha a bemenetek minden kombinációja esetén az egyik bemenet hamisról igazra való váltása csak azt eredményezheti, hogy a kimenet hamisról igazra vált, és nem igazról hamisra. Grafikailag ez azt jelenti, hogy egy n -aril Boole-függvény monoton, ha annak ábrázolása, mint egy n -cube jelzett igazság értékeket nem felfelé széle igaz , hogy hamis . (Ezt a jelzett Hasse rajz a kettős a függvény jelzett Venn-diagram , amely a leggyakoribb képviseletét n ≤ 3 .)

A monoton Boole-függvények pontosan azok, amelyek lehet meghatározni egy kifejezés egyesíti a bemenetek (amelyek valószínűleg többször), csak a szereplők és és vagy (különösen nem tilos). Például "legalább két olyan , b , c hold" egy monoton függvénye egy , b , c , mert lehet írva például ahogy (( a és b ), vagy ( a és c ), vagy ( b és c )).

A számos ilyen funkciók n változók ismert, mint a Dedekind számát a n .

Lásd még

• Monoton köbös interpoláció
• Ál-monoton operátor
• Spearman rangkorrelációs együtthatója - a monotonitás mértéke egy adathalmazban
• Teljes monotonitás
• Ciklikus monotonitás
• Kezelői monoton funkció

Megjegyzések

Bibliográfia

• Bartle, Robert G. (1976). A valódi elemzés elemei (második szerk.).
• Grätzer, George (1971). Rácselmélet: első fogalmak és elosztó rácsok . ISBN 0-7167-0442-0.
• Pemberton, Malcolm; Rau, Nicholas (2001). Matematika közgazdászoknak: bevezető tankönyv . Manchester University Press. ISBN 0-7190-3341-1.
• Renardy, Michael & Rogers, Robert C. (2004). Bevezetés a parciális differenciálegyenletekbe . Szövegek az alkalmazott matematikában 13 (második kiadás). New York: Springer-Verlag. o. 356. ISBN 0-387-00444-0.
• Riesz, Frigyes & Szőkefalvi-Nagy Béla (1990). Funkcionális elemzés . Courier Dover Publications. ISBN 978-0-486-66289-3.
• Russell, Stuart J .; Norvig, Péter (2010). Mesterséges intelligencia: modern megközelítés (3. kiadás). Upper Saddle River, New Jersey: Prentice Hall. ISBN 978-0-13-604259-4.
• Simon, Carl P .; Blume, Lawrence (1994. április). Matematika közgazdászoknak (első szerk.). ISBN 978-0-393-95733-4. (9.31. Definíció)

Külső linkek

• "Monoton funkció" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Anik Debnath és Thomas Roxlo (The Harker School) monoton szekvenciájának konvergenciája , Wolfram Demonstrations Project .
• Weisstein, Eric W. "Monoton funkció" . MathWorld .