Piros -fekete fa - Red–black tree

Vörös -fekete fa
típus	fa
Feltalált	1972
Feltalálta	Rudolf Bayer
Időbonyolultsága az o jelölés
Algoritmus Átlagos Legrosszabb esetben Tér ${\ displaystyle {\ mathcal {O}} (n)}$ ${\ displaystyle {\ mathcal {O}} (n)}$ Keresés ${\ displaystyle {\ mathcal {O}} (\ log n)}$ ${\ displaystyle {\ mathcal {O}} (\ log n)}$ Beszúrás amortizálódott ${\ displaystyle {\ mathcal {O}} (1)}$ ${\ displaystyle {\ mathcal {O}} (\ log n)}$ Töröl amortizálódott ${\ displaystyle {\ mathcal {O}} (1)}$ ${\ displaystyle {\ mathcal {O}} (\ log n)}$

Az informatikában a vörös-fekete fa egyfajta önegyensúlyozó bináris keresési fa . Mindegyik csomópont tárol egy extra bitet, amely a "színt" ("piros" vagy "fekete") képviseli, ezzel biztosítva, hogy a fa egyensúlyban maradjon a beszúrások és törlések során.

Amikor a fát módosítják, az új fát átrendezik és "átfestik", hogy visszaállítsák azokat a színező tulajdonságokat, amelyek korlátozzák a fa egyensúlytalanságát a legrosszabb esetben. A tulajdonságokat úgy alakították ki, hogy ez az átrendezés és újrafestés hatékonyan elvégezhető legyen.

Az újraegyensúlyozás nem tökéletes, de garantálja az időben történő keresést , hol van a fa csomópontjainak száma. A beillesztési és törlési műveleteket, valamint a fa átrendeződését és átszínezését is időben elvégzik . ${\ displaystyle {\ mathcal {O}} (\ log n)}$${\ displaystyle n}$${\ displaystyle {\ mathcal {O}} (\ log n)}$

Az egyes csomópontok színének követése csomópontonként csak egy bit információt igényel, mivel csak két szín létezik. A fa nem tartalmaz más, vörös -fekete fára jellemző adatokat, így memóriaterülete szinte megegyezik egy klasszikus (színtelen) bináris keresőfával . Sok esetben a további információmennyiség további memóriaköltség nélkül tárolható.

Történelem

1972-ben Rudolf Bayer feltalált egy adatstruktúrát, amely a B-fa speciális, 4-es rendje volt . Ezek a fák a gyökértől a levélig minden utat fenntartottak ugyanannyi csomóponttal, tökéletesen kiegyensúlyozott fákat hozva létre. Ezek azonban nem bináris keresőfák voltak. Bayer „szimmetrikus bináris B-fának” nevezte őket, és később 2-3–4 vagy csak 2–4 fa néven váltak népszerűvé .

Leonidas J. Guibas és Robert Sedgewick egy 1978-as "A Dichromatic Framework for Balanced Frees " című dokumentumban a vörös-fekete fát a szimmetrikus bináris B-fából származtatta. A "vörös" színt azért választották, mert ez volt a legjobb megjelenésű szín, amelyet a Xerox PARC- nál dolgozva a szerzők rendelkezésére álló színes lézernyomtató állított elő . Guibas másik válasza szerint a fák rajzolásához rendelkezésre álló piros és fekete tollak miatt történt.

1993 -ban Arne Andersson bevezette a jobbra dőlő fa ötletét a beszúrási és törlési műveletek egyszerűsítése érdekében.

1999 -ben Chris Okasaki megmutatta, hogyan lehet a betétet tisztán működőképessé tenni. Kiegyensúlyozási funkciójának csak 4 kiegyensúlyozatlan eset és egy alapértelmezett kiegyensúlyozott eset kezelésére volt szüksége.

Az eredeti algoritmus 8 kiegyensúlyozatlan esetet használt, de Cormen et al. (2001) ezt 6 kiegyensúlyozatlan esetre csökkentette. Sedgewick megmutatta, hogy a beillesztési művelet mindössze 46 sor Java kódban valósítható meg. 2008-ban Sedgewick javasolta a balra dőlő piros-fekete fát , kihasználva Andersson ötletét, amely egyszerűsítette a beillesztési és törlési műveleteket. Sedgewick eredetileg megengedte azokat a csomópontokat, amelyeknek két gyermeke vörös, így a fái inkább 2-3–4 fának tűnnek, de később ezt a korlátozást hozzáadták, így az új fák inkább 2-3 fának számítottak. Sedgewick mindössze 33 sorban valósította meg a beszúrási algoritmust, jelentősen lerövidítve eredeti 46 sorát.

Terminológia

Példa egy vörös -fekete fára

1. ábra: ... explicit NIL levelekkel

2. ábra: ... implicit bal és jobb dokkolópontokkal

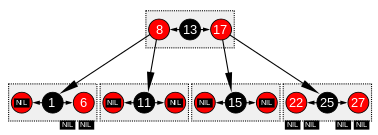
A vörös -fekete fa egy speciális típusú bináris keresőfa , amelyet az informatikában használnak összehasonlítható adatok , például szövegrészek vagy számok rendszerezésére (például az 1. és 2. ábrán szereplő számok). A kulcsokat és/vagy adatokat hordozó csomópontokat gyakran "belső csomópontoknak" nevezik , de ennek nagyon specifikussága érdekében ebben a cikkben nem NIL csomópontoknak is nevezik őket.

A vörös -fekete fák levélcsomópontjai ( NIL az 1. ábrán) nem tartalmaznak kulcsokat vagy adatokat. Ezeknek a „leveleknek” nem kell kifejezetten egyének lenniük a számítógép memóriájában: a NULL -mutató - mint minden bináris fa adatstruktúrában - kódolhatja azt a tényt, hogy nincs (utód) csomópont ezen a helyen a (szülő) csomópontban. Mindazonáltal a fában elfoglalt helyük alapján ezek az objektumok más csomópontokhoz vannak viszonyítva, amelyek relevánsak az RB-szerkezet szempontjából, lehetnek szülei, testvérei (azaz a szülő másik gyermeke), nagybátyja, sőt unokaöccse csomópont; és lehet gyermek, de soha nem lehet más csomópont szülője. Valójában nem szükséges "színt" rendelni ezekhez az útvégi objektumokhoz, mert az "is " vagy " feltételre utal az" is "feltétel (lásd még ezt a megjegyzést ).   NILBLACKNIL

A 2. ábra szemlélteti ugyanazt a vörös -fekete fát, NIL levelek nélkül. Annak érdekében, hogy megkapjuk az azonos fogalma egy utat , az egyik, hogy észre, hogy pl 3 utak fut át a csomópont 1 , nevezetesen egy ösvényt 1 _maradt plusz 2 utak révén 1 _jobbra , azaz a utak révén 6 _bal és 6 _jobbra . Ily módon ezek az útvonalak dokkolópontok az új csomópontok beillesztéséhez, amelyek teljesen megfelelnek az 1. ábra NIL leveleinek.

Másrészt, a végrehajtási idő marginális megtakarítása érdekében ezeket (esetleg sok) NIL leveleket mutatóként lehet megvalósítani egyetlen egyedi (és fekete) őrszemcsomópontra ( a NULL értékű mutatók helyett ).

Következtetésként elmondható, hogy az a tény, hogy egy gyermek nem létezik (nem valódi csomópont, nem tartalmaz adatokat), minden esetben ugyanazzal a NULL -mutatóval vagy ugyanazzal a mutatóval határozható meg. Ebben a cikkben bármelyik lehetőséget NIL csomópontnak nevezik, és állandó értéke van NIL .

A csomópont fekete mélységét a gyökértől a csomópontig terjedő fekete csomópontok számának (azaz a fekete ősök számának) határozzák meg. A vörös -fekete fa fekete magassága a fekete csomópontok száma a gyökértől a levelekig tartó bármely útvonalon, amely a 4. követelmény szerint állandó (alternatívaként bármelyik levélcsomópont fekete mélységeként definiálható). A csomópont fekete magassága az általa gyökerezett részfa fekete magassága. Ebben a cikkben egy NIL csomópont fekete magasságát 0 -ra kell állítani, mert a részfa üres, amint azt a 2. ábra javasolja, és a fa magassága is 0.

Tulajdonságok

A bináris keresőfával szemben támasztott követelményeken túl a piros -fekete fának is meg kell felelnie :

1. Minden csomópont piros vagy fekete.
2. Minden NIL csomópont (1. ábra) feketének számít.
3. A piros csomópontnak nincs vörös gyermeke.
4. Egy adott csomóponttól a leszármazott NIL csomópontjaihoz vezető minden út azonos számú fekete csomóponton megy keresztül.

Egyes szerzők, például Cormen és társai, ötödik követelményként azt állítják, hogy "a gyökér fekete"; de nem Mehlhorn & Sanders vagy Sedgewick & Wayne. Mivel a gyökér mindig vörösről feketére változtatható, ez a szabály kevés hatással van az elemzésre. Ez a cikk is kihagyja, mert kissé zavarja a rekurzív algoritmusokat és bizonyításokat.

Például minden tökéletes bináris fa, amely csak fekete csomópontokból áll, vörös -fekete fa.

A csak olvasható műveletek, például a keresés vagy a fa bejárása, nem érintik a követelményeket. Másrészt a módosító műveletek könnyen beszúrják és törlik az 1. és 2. követelményeket, de a többi követelményhez képest további erőfeszítéseket kell tenni annak érdekében, hogy elkerüljük a 3. követelmény megsértésének bevezetését.piros megsértése , vagy a 4. követelmény, az úgynevezett afekete-szabálysértés .

A követelmények a vörös -fekete fák kritikus tulajdonságait érvényesítik: a gyökértől a legtávolabbi levélig vezető út legfeljebb kétszer olyan hosszú, mint a gyökértől a legközelebbi levélig vezető út . Ennek eredményeként a fa magassága kiegyensúlyozott . Mivel az olyan műveletekhez, mint az értékek beillesztése, törlése és megkeresése , a fa magasságával arányos legrosszabb esetre van szükség , ez a felső határ a magasságban lehetővé teszi, hogy a vörös-fekete fák a legrosszabb esetben is hatékonyak legyenek, nevezetesen logaritmikus a csomópontok számában , azaz ez nem jellemző a bináris keresőfákra . Matematikai bizonyítékért lásd a Határok igazolása című részt . ${\ displaystyle h}$${\ displaystyle n}$${\ displaystyle h \ in {\ mathcal {O}} (\ log n)}$

A vörös-fekete fák, mint minden bináris keresőfa , meglehetősen hatékony szekvenciális hozzáférést tesznek lehetővé (pl . Sorrendben való bejárás , azaz: Bal – Gyökér – Jobb sorrendben) elemeikhez. De aszimptotikusan optimális közvetlen hozzáférést is támogatnak a gyökértől a levélig való áthaladáson keresztül, ami keresési időt eredményez. ${\ displaystyle {\ mathcal {O}} (\ log n)}$

Hasonlóan a B rendű fákhoz 4

3. ábra: Ugyanaz a piros-fekete fa, mint a fenti példában, most B-fa

A vörös-fekete fa szerkezete hasonló a 4 -es rendű B-fához , ahol minden csomópont 1-3 értéket és (ennek megfelelően) 2-4 gyermekmutatót tartalmazhat. Egy ilyen B-fában minden csomópont csak egy értéket fog tartalmazni, amely megfelel a vörös-fekete fa fekete csomópontjának értékének, opcionális értékkel előtte és/vagy utána ugyanabban a csomópontban, mindkettő megegyezik a a piros -fekete fa.

Ennek az egyenértékűségnek az egyik módja a vörös csomópontok "felfelé mozgatása" a piros -fekete fa grafikus ábrázolásában, hogy vízszintesen igazodjanak a szülő fekete csomóponthoz, egy vízszintes klaszter létrehozásával. A B-fában vagy a vörös-fekete fa módosított grafikus ábrázolásában minden levélcsomópont azonos mélységben van.

A vörös-fekete fa ekkor szerkezetileg megegyezik a 4-es rendű B-fával, minimális kitöltési tényezője az értékek 33% -a fürtönként, maximális kapacitása pedig 3 érték.

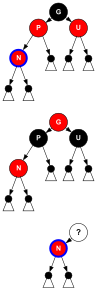
Ez a B-fa típus azonban még általánosabb, mint a vörös-fekete fa, mivel lehetővé teszi a kétértelműséget a vörös-fekete fa átalakításban-több vörös-fekete fa is előállítható a 4. rendű B-fából (lásd a 3. ábrát) ). Ha egy B-fa-fürt csak 1 értéket tartalmaz, akkor ez a minimum, fekete, és két utómutatóval rendelkezik. Ha egy fürt 3 értéket tartalmaz, akkor a középső érték fekete lesz, és minden oldalán tárolt érték piros lesz. Ha azonban a fürt két értéket tartalmaz, akkor bármelyik a piros -fekete fa fekete csomópontjává válhat (a másik pedig piros lesz).

Tehát a 4-es rendű B-fa nem tartja fenn, hogy az egyes klaszterekben szereplő értékek közül melyik a gyökér fekete fa az egész fürtre és a többi érték szülője ugyanabban a fürtben. Ennek ellenére a vörös -fekete fákon végzett műveletek időben gazdaságosabbak, mivel nem kell fenntartani az értékek vektorát. Drága lehet, ha az értékeket közvetlenül minden csomópontban tároljuk, nem pedig hivatkozás alapján. A B-fa csomópontok azonban gazdaságosabbak a térben, mivel nem kell tárolni az egyes csomópontok szín attribútumát. Ehelyett tudnia kell, hogy a fürtvektor melyik rését használja. Ha az értékeket hivatkozás alapján tároljuk, pl. Objektumokat, akkor null hivatkozások használhatók, és így a fürt egy vektorral ábrázolható, amely 3 rést tartalmaz az értékmutatókra és 4 rést a fán lévő gyermekhivatkozásokra. Ebben az esetben a B-fa kompaktabb lehet a memóriában, javítva az adatok helyét.

Ugyanez az analógia állítható elő a nagyobb megrendelésű B-fákkal, amelyek szerkezetileg egyenértékűek lehetnek egy színes bináris fával: csak több színre van szüksége. Tegyük fel, hogy hozzáadja a kéket, majd a kék -piros -fekete fát, mint a piros -fekete fákat, de azzal a további megkötéssel, hogy a hierarchia két egymást követő csomópontja nem lesz kék, és minden kék csomópont egy piros csomópont gyermeke lesz, majd egyenértékűvé válik egy B-fával, amelynek fürtjei legfeljebb 7 értékkel rendelkeznek a következő színekben: kék, piros, kék, fekete, kék, piros, kék (Minden klaszterben legfeljebb 1 fekete csomópont, 2 piros csomópont lesz és 4 kék csomópont).

Mérsékelt mennyiségű érték esetén a színes bináris fába való beillesztések és törlések gyorsabbak a B-fákhoz képest, mivel a színes fák nem próbálják maximalizálni a csomópontok vízszintes csoportjainak kitöltési tényezőjét (csak a minimális kitöltési tényező garantált színes bináris fájlban) fák, korlátozva a hasadékok számát vagy a fürtök csomópontjait). A B-fák gyorsabban hajtják végre a forgatást (mivel a forgatások gyakran ugyanazon a fürtön belül fordulnak elő, nem pedig több különálló csomóponttal egy színes bináris fában). Nagy mennyiségű tárolás esetén azonban a B-fák sokkal gyorsabbak lesznek, mivel kompaktabbak lesznek, ha több gyermeket csoportosítanak ugyanabba a klaszterbe, ahol helyileg hozzáférhetők.

A B-fák minden lehetséges optimalizálása a fürtök átlagos kitöltési tényezőinek növelése érdekében lehetséges az ekvivalens többszínű bináris fában. Nevezetesen, az átlagos kitöltési tényező maximalizálása egy szerkezetileg ekvivalens B-fában ugyanaz, mint a többszínű fa teljes magasságának csökkentése a nem fekete csomópontok számának növelésével. A legrosszabb eset akkor fordul elő, ha egy színes bináris fa összes csomópontja fekete, a legjobb esetben, ha csak egyharmada fekete (a másik kétharmada pedig piros csomópont).

Alkalmazások és kapcsolódó adatstruktúrák

A vörös-fekete fák a legrosszabb esetben garanciát nyújtanak a beillesztési, törlési és keresési időre. Ez nemcsak értékessé teszi őket az időérzékeny alkalmazásokban, például a valós idejű alkalmazásokban , hanem értékes építőkövekké teszi azokat más adatstruktúrákban, amelyek a legrosszabb esetek garanciáját nyújtják; például a számítási geometriában használt sok adatstruktúra vörös -fekete fákon alapulhat, a jelenlegi Linux kernelekben és az epoll rendszerhívás -implementációban használt Teljesen korrekt ütemező pedig vörös -fekete fákat használ.

Az AVL fa egy másik struktúra, amely támogatja a keresést, beillesztést és eltávolítást. Az AVL fák vörös -fekete színűek lehetnek, így az RB fák részhalmaza. A legrosszabb magasság 0,720-szorosa az RB fák legrosszabb magasságának, így az AVL fák merevebben kiegyensúlyozottak. Ben Pfaff teljesítménymérései 79 futtatásban reális tesztesetekkel 0,677 és 1,077 közötti AVL / RB arányt, 0,947 mediánt és 0,910 geometriai átlagot találnak. A WAVL fák teljesítménye e kettő között van. ${\ displaystyle {\ mathcal {O}} (\ log n)}$

A vörös -fekete fák különösen értékesek a funkcionális programozásban is , ahol az egyik leggyakoribb állandó adatstruktúra , amelyet asszociatív tömbök és halmazok létrehozására használnak , amelyek a mutációk után is megőrzik korábbi verzióikat. A vörös -fekete fák tartós változata időt és időt igényel minden beillesztéshez vagy törléshez. ${\ displaystyle {\ mathcal {O}} (\ log n)}$

Minden 2–4 fa esetében vannak megfelelő piros -fekete fák, amelyek azonos sorrendben vannak adatelemekkel. A 2–4 fára történő beillesztési és törlési műveletek szintén megfelelnek a piros-fekete fák színcserélésének és forgatásának. Ezáltal a 2–4 ​​fa fontos eszköz a vörös -fekete fák mögött rejlő logika megértéséhez, és ezért sok bevezető algoritmusszöveg 2–4 fát vezet be közvetlenül a piros – fekete fák előtt, annak ellenére, hogy 2–4 fát nem gyakran használnak gyakorlat.

2008-ban Sedgewick bevezette a vörös-fekete fa egyszerűbb változatát, az úgynevezett balra dőlő piros-fekete fát azáltal, hogy megszüntette a végrehajtás korábban nem meghatározott szabadságfokát. Az LLRB további invariánst tart fenn, amely szerint minden piros láncszemnek balra kell dőlnie, kivéve a behelyezéseket és a törléseket. A vörös -fekete fák izometrikusak lehetnek 2-3 fára vagy 2–4 fára, bármilyen műveletsor esetén. A 2–4 fa izometriát 1978 -ban írta le Sedgewick. 2–4 fával az izometriát egy felosztásnak megfelelő „színfordítás” oldja fel, amelyben két gyermekcsomópont vörös színe elhagyja a gyermekeket, és a szülőcsomópontba kerül.

A tangófa eredeti leírása , amely a gyors keresésekre optimalizált fa, kifejezetten vörös -fekete fákat használ az adatszerkezet részeként.

Mivel a Java 8, a HashMap módosításra került oly módon, hogy ahelyett, hogy egy láncolt lista tárolni a különböző elemeket ütközik hashcodes , piros-fekete fát használnak. Ez azt eredményezi, hogy az ilyen elemek keresésének időbeli összetettsége javul, és honnan van az ütköző hashcode -okkal rendelkező elemek száma. ${\ displaystyle {\ mathcal {O}} (m)}$${\ displaystyle {\ mathcal {O}} (\ log m)}$${\ displaystyle m}$

Tevékenységek

A csak olvasható műveletek, mint például a keresés vagy a fa bejárása, egy vörös-fekete fán nem igényelnek módosítást a bináris keresési fákhoz használt műveletekhez képest , mivel minden piros-fekete fa egy egyszerű bináris keresőfa különleges esete. A behelyezés vagy eltávolítás azonnali eredménye azonban megsértheti a vörös-fekete fa tulajdonságait, amelynek helyreállítását egyensúlyba állításnak nevezik , hogy a vörös-fekete fák önkiegyenlítődjenek. Ez megköveteli a legrosszabb esetben egy kis számú, az o jelölés , ahol a szám a tárgyak a fa, átlagosan vagy amortizált , állandó számú, a színváltozás (amely nagyon gyorsan a gyakorlatban); és legfeljebb három faforgatás (kettő a beillesztéshez). ${\ displaystyle {\ mathcal {O}} (\ log n)}$${\ displaystyle n}$ ${\ displaystyle {\ mathcal {O}} (1)}$

Ha az alábbi példa implementáció nem megfelelő, akkor más megvalósítások magyarázattal megtalálhatók Ben Pfaff jegyzetekkel ellátott C könyvtárában, a GNU libavl -ban (v2.0.3, 2019 június).

A behelyezési és eltávolítási műveletek részleteit a C ++ kód példájával mutatjuk be . A példakód felkérheti az alábbi segítő funkciókat, hogy megtalálják a szülő, nagyszülő, nagybácsi, testvér és unokaöccse csomópontokat, és balra vagy jobbra forgathassanak egy részfát:

// Basic type definitions:

enum color_t { BLACK, RED };

struct RBnode {     // node of red–black tree
  RBnode* parent;   // == NULL if root of the tree
  RBnode* child[2]; // == NIL if child is empty
    // Index is:
    //   LEFT  := 0, if (key < parent->key)
    //   RIGHT := 1, if (key > parent->key)
  enum color_t color;
  int key;
};

#define NIL   NULL // null pointer  or  pointer to sentinel node
#define LEFT  0
#define RIGHT 1
#define left  child[LEFT]
#define right child[RIGHT]

struct RBtree { // red–black tree
  RBnode* root; // == NIL if tree is empty
};

// Get the child direction (∈ { LEFT, RIGHT })
//   of the non-root non-NIL  RBnode* N:
#define childDir(N) ( N == (N->parent)->right ? RIGHT : LEFT )

// Helper functions:

RBnode* GetParent(RBnode* N) {
  // The parent of the root node is set to NULL.
  return N == NULL ? NULL : N->parent;
}

RBnode* GetGrandParent(RBnode* N) {
  // Will return NULL if N is root or child of root
  return GetParent(GetParent(N));
}

RBnode* GetSibling(RBnode* N) {
  RBnode* P = GetParent(N);
  // No parent means no sibling:
  assert(P != NULL);
  return P->child[1-childDir(N)];
}
// If parent P and child direction dir is available, same as:
//   P->child[1-dir]

RBnode* GetUncle(RBnode* N) {
  RBnode* P = GetParent(N);
  // No parent means no uncle:
  assert(P != NULL);
  return GetSibling(P);
}

RBnode* GetCloseNephew(RBnode* N) {
  RBnode* P = GetParent(N);
  int dir;
  RBnode* S;
  assert(P != NULL);
  dir = childDir(N);
  S = P->child[1-dir]; // sibling of N
  assert(S != NIL);
  return S->child[dir]; // the nephew close to N
}

RBnode* GetDistantNephew(RBnode* N) {
  RBnode* P = GetParent(N);
  int dir;
  RBnode* S;
  assert(P != NULL);
  dir = childDir(N);
  S = P->child[1-dir]; // sibling of N
  assert(S != NIL);
  return S->child[1-dir]; // the nephew distant from N
}

RBnode* RotateDirRoot(
    RBtree* T,   // red–black tree
    RBnode* P,   // root of subtree (may be the root of T)
    int dir) {   // dir ∈ { LEFT, RIGHT }
  RBnode* G = P->parent;
  RBnode* S = P->child[1-dir];
  RBnode* C;
  assert(S != NIL); // pointer to true node required
  C = S->child[dir];
  P->child[1-dir] = C; if (C != NIL) C->parent = P;
  S->child[  dir] = P; P->parent = S;
  S->parent = G;
  if (G != NULL)
    G->child[ P == G->right ? RIGHT : LEFT ] = S;
  else
    T->root = S;
  return S; // new root of subtree
}

#define RotateDir(N,dir) RotateDirRoot(T,N,dir)
#define RotateLeft(N)    RotateDirRoot(T,N,LEFT)
#define RotateRight(N)   RotateDirRoot(T,N,RIGHT)

Megjegyzések a mintakódhoz és a behelyezés és eltávolítás diagramjaihoz

A javaslat mind a beillesztést, mind az eltávolítást (néhány nagyon egyszerű esetet nem említve) hat csomópont, élek és szín konstellációra bontja, amelyeket eseteknek nevezünk. Az esetek esetleges javítása (újraegyensúlyozása) néha egy későbbi eset kódját használja. A javaslat mind a behelyezésre, mind az eltávolításra vonatkozóan pontosan egy olyan esetet tartalmaz, amely egy fekete szintet közelebb visz a gyökérhez és a hurkokhoz, a másik öt eset pedig egyensúlyba hozza saját fáját. A bonyolultabb eseteket egy diagram mutatja.

• A változó Naz aktuális csomópontot jelöli, amelyet a diagramok N jelöléssel látnak el.
• egy piros csomópontot és egy (nem NIL) fekete csomópontot jelképez (fekete magasság ≥ 1), a (nem NIL) csomópont lehet piros vagy fekete, de ugyanazon színű ugyanazon a diagramon. Az igazi NIL csomópontok nincsenek ábrázolva a diagramokon.
• A diagram három oszlopot és két -négy műveletet tartalmaz.
  • A bal oldali oszlop az első iterációt mutatja, a jobb oszlop a magasabb iterációkat, a középső oszlop az eset szegmentálását mutatja a különböző műveletekre.
  1. A "bejegyzés" művelet a csomópontok konstellációját mutatja színeikkel, amelyek meghatározzák az esetet, és többnyire megsértenek néhány követelményt .
     Kék szegély gyűrűk az aktuális csomópont N , és a többi csomópont vannak címkézve aszerint, hogy azok kapcsolatban N .
  2. Ha a forgatást hasznosnak ítélik, ezt a következő művelet mutatja be, amelyet "forgatás" felirattal látunk el.
  3. Ha néhány újrafestést hasznosnak tartanak, akkor ezt a következő művelet mutatja be, amely "szín" címkével van ellátva.
  4. Ha még mindig szükség van javításra, a konstelláció kielégíti a beszúrás vagy törlés ciklus invariánsát az újonnan hozzárendelt aktuális N csomóponttal , amely ezután ismét kék gyűrűt hordoz. Valószínűleg néhány más csomópont is újonnan van hozzárendelve N -hez képest . Ez a művelet "újrarendelés" címkével rendelkezik.
     A későbbi műveletek újrafelhasználják a többi eset kódját, amelyek szintén a gyökérhez közelebb eső fekete szinttel ismétlődhetnek.
• Az esetlegesen számozott háromszög, amelynek tetején fekete kör látható, egy piros -fekete részfát jelent (a szülőhöz a 3. követelmény szerint csatlakozik ), amelynek fekete magassága megegyezik az iterációs szint mínusz eggyel, azaz nullával az első iterációban. Gyökere vörös vagy fekete lehet.
  Egy lehetséges számozott háromszög egy piros -fekete részfát jelent, eggyel kevesebb fekete magassággal, azaz szülője fekete nulla magasságú a második iterációban.

Megjegyzés

Az egyszerűség kedvéért a mintakód a diszjunkciót használja :

U == NIL || U->color == BLACK // considered black

és a kötőszó :

U != NIL && U->color == RED   // not considered black

Ezáltal szem előtt kell tartani, hogy mindkét állítást nem értékelik összesen, ha U == NIL. Ezután mindkét esetben U->colornem érinti (lásd Rövidzárlat-értékelés ).
(A megjegyzés considered blackmegfelel a 2. követelménynek .)

A kapcsolódó ifállítások sokkal ritkábban fordulnak elő, ha a javaslatot megvalósítják.

Beillesztés

A beszúrás azzal kezdődik, hogy az új (nem NIL) csomópontot, mondjuk N-t , egy olyan NIL-csomópont bináris keresési fájának pozíciójába helyezzük, amelynek sorrendben az előd kulcsa kevesebbet hasonlít, mint az új csomópont kulcsa, ami viszont kevesebbet, mint a kulcs. rendben lévő utódjának. (Gyakran ez a pozicionálás az eredménye egy keresési belül a fa közvetlenül megelőző betét működését, és egy csomópont Pegyütt irány dira P->child[dir] == NIL.) Az újonnan beillesztett csomópont ideiglenesen piros színű, így minden út tartalmazza az azonos számú fekete csomópontok mint azelőtt. De ha a szülője, mondjuk P , szintén vörös, akkor ez a művelet piros szabálysértést vezet be .

void RBinsert1(
  RBtree* T,         // -> red–black tree
  struct RBnode* N,  // -> node to be inserted
  struct RBnode* P,  // -> parent node of N ( may be NULL )
  byte dir)          // side ( LEFT or RIGHT ) of P where to insert N
{
  struct RBnode* G;  // -> parent node of P
  struct RBnode* U;  // -> uncle of N

  N->color = RED;
  N->left  = NIL;
  N->right = NIL;
  N->parent = P;
  if (P == NULL) {   // There is no parent
    T->root = N;     // N is the new root of the tree T.
    return; // insertion complete
  }
  P->child[dir] = N; // insert N as dir-child of P
  // start of the (do while)-loop:
  do {

Az egyensúlyozó hurok a következő változatlan :

• A jelenlegi csomópont N jelentése (piros) elején minden egyes iteráció.
• A 3. követelmény minden pár csomópont ← szülő számára teljesül, az esetleges N ← P kivétellel, ha P is piros ( N - nél piros megsértés ).
• Az összes többi tulajdonság (beleértve a 4. követelményt is ) teljesül a fán.

Megjegyzések a beillesztési diagramokhoz

előtt

eset →

forgatóberende- CIÓ

assig- nment

után

→ következő

Δh

P

G

U

x

P

G

U

x

-

I3

→

I1

→

-

I4

→

I2

N : = G

?

?

2

én

I5

P ↶ N.

N : = P

o

I6

0

o

I6

P ↷ G

→

Beillesztés: Ez a szinopszis az előtti oszlopban azt mutatja , hogy                 a konstellációk minden lehetséges esete le van fedve.

• Az ábrákon P a N szülő, G a nagyszülő, U pedig N nagybátyját jelenti.
• A diagramokon a P szülőcsomópont G szülőjének bal gyermeke látható, annak ellenére, hogy lehetséges, hogy P mindkét oldalon van. A mintakód mindkét lehetőséget lefedi az oldalsó változó segítségével dir.
• N a beszúrási csomópont, de a művelet előrehaladtával más csomópontok is aktuálissá válhatnak (lásd az I2 esetet ).
• A diagramok azokat az eseteket is mutatják, amikor P is piros, a piros megsértést.
• Az x oszlop a gyermek irányának változását jelzi, azaz az o ("külső" esetén azt jelenti, hogy P és N egyaránt bal vagy mindkét jobb gyermek, míg i ("belső") azt jelenti, hogy a gyermek iránya P -ről N „s.
• Az előző oszlopcsoport meghatározza az esetet, amelynek nevét az oszlop kis- és nagybetűiben adja meg . Ezáltal az üresen hagyott cellák lehetséges értékeit figyelmen kívül hagyja. Tehát az I2 esetben a mintakód mindkét N gyermekirányú lehetőséget lefedi , bár a megfelelő diagram csak egyet mutat.
• A szinopszis sorai úgy vannak elrendezve, hogy az összes lehetséges RB eset lefedettsége könnyen érthető legyen.
• Az oszlopot forgatás jelzi, hogy a forgatás hozzájárul a kiegyensúlyozás.
• Az oszlop hozzárendelése N hozzárendelést mutat, mielőtt belép egy következő lépésbe. Ez valószínűleg a többi P , G , U csomópont átrendelését is előidézi .
• Ha valami megváltozott a helyzet, ezt mutatja az oszlop csoport után .
• A nyíl → a következő oszlopban azt jelzi, hogy ezzel a lépéssel befejeződött az újraegyensúlyozás. Ha az utólagos oszlop pontosan egy esetet határoz meg, akkor ezt az esetet adjuk meg következőként, különben kérdőjelek vannak.
• A hurok az "Insert case 1" és a "Insert case 2" szekciókban található , ahol az I2 esetben az újraegyensúlyozás problémája magasabb szintre emelkedik a fán, úgy, hogy a G nagyapa lesz az új aktuális N csomópont . Tehát a fa (hol van a fa magassága) javítása maximális iterációt igényel . Mivel az eszkaláció valószínűsége exponenciálisan csökken minden iterációval, a teljes újraegyensúlyozási költség átlagosan állandó, de amortizált állandó .${\ displaystyle \ Delta h = 2}$${\ displaystyle {\ tfrac {h} {2}}}$${\ displaystyle h}$
• A hurok törzséből az I1 eset önmagában kilép, és vannak kilépő ágak az I4 , I6 , I5 + I6 és I3 esetekhez .
• Forgások fordulnak elő az I6 és I5 + I6 esetekben - a hurkon kívül. Ezért összesen legfeljebb két forgatás fordul elő.

Helyezze be a tokot 1

Az aktuális csomópont szülője P fekete, így a 3. követelmény érvényes. 4. követelmény tartja továbbá szerinti hurok invariáns .

    if (P->color == BLACK) {
      // Case_I1 (P black):
      return; // insertion complete
    }
    // From now on P is red.
    if ((G = GetParent(P)) == NULL) 
      goto Case_I4; // P red and root
    // else: P red and G!=NULL.
    dir = childDir(P); // the side of parent G on which node P is located
    U = G->child[1-dir]; // uncle
    if (U == NIL || U->color == BLACK) // considered black
      goto Case_I56; // P red && U black

első iteráció

nagyobb iteráció

Helyezze be a tokot 2

Helyezze be a tokot 2

Ha mind a P szülő, mind az U nagybácsi vörös, akkor mindkettő átfesthető feketére, és G nagyszülő vörösre vált a 4. követelmény fenntartása érdekében . Mivel a szülőn vagy bácsin keresztül vezető útnak a nagyszülőn kell áthaladnia, ezeken az utakon a fekete csomópontok száma nem változott. Azonban a nagyszülő G most sérti követelmény 3, ha van egy vörös szülő. A G – N átcímkézés után a hurok invariáns teljesül, így az egyensúlyozás egy fekete szinttel (= 2 fa szinttel) magasabbra iterálható.

    // Case_I2 (P+U red):
    P->color = BLACK;
    U->color = BLACK;
    G->color = RED;
    N = G; // new current node
    // iterate 1 black level
    //   (= 2 tree levels) higher
  } while ((P = N->parent) != NULL);
  // end of the (do while)-loop

Helyezze be a tokot 3

Az aktuális N csomópont a fa gyökere, és minden RB-tulajdonság megelégszik az N piros gyökérrel .

  // Case_I3 (P == NULL):
  return; // insertion complete

Helyezze be a tokot 4

A P szülő vörös és a gyökér. Mivel N is piros, a 3. követelményt megsértik. De a P szín megváltoztatása után a fa RB alakú. A fa fekete magassága 1 -gyel nő.

Case_I4: // P is the root and red:
  P->color = BLACK;
  return; // insertion complete

első iteráció

nagyobb iteráció

Helyezze be a tokot 5

Helyezze be a tokot 5

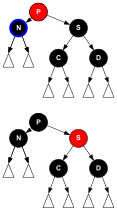
A szülő P vörös, de az U nagybácsi fekete. A végső cél az, hogy a P szülőcsomópontot a nagyszülő pozícióba forgassa , de ez nem fog működni, ha N G "belső" unokája (azaz ha N a G jobb gyermekének bal gyermeke vagy a G ) bal gyermeke . Egy dir-rotation a P kapcsolók szerepét az aktuális csomópont N és a szülő P . A forgatás útvonalakat ad hozzá az N -hez (a 2 -es alfában lévőket , lásd az ábrát), és eltávolítja a P -n keresztül vezető utakat (a 4 -es alfában lévőket ). De mind P, mind N piros, így a 4. követelmény megmarad. A 3. követelmény visszaáll a 6. esetben.

Case_I56: // P red && U black:
  if (N == P->child[1-dir])
  { // Case_I5 (P red && U black && N inner grandchild of G):
    RotateDir(P,dir); // P is never the root
    N = P; // new current node
    P = G->child[dir]; // new parent of N
    // fall through to Case_I6
  }

első iteráció

nagyobb iteráció

Helyezze be a tokot 6

Helyezze be a tokot 6

Az aktuális N csomópont most már biztos, hogy G "külső" unokája (bal gyermek bal vagy jobb gyermek jobbja). Most (1-dir)-rotate a G , amivel a P helyett a G , és így a P a szülő a N és G . G fekete, korábbi gyermeke P vörös, mivel megsértették a 3. követelményt . A P és G színének megváltoztatása után a kapott fa megfelel a 3. követelménynek. A 4. követelmény is teljesül, mivel a fekete G -n áthaladó összes út most a fekete P -n megy keresztül .

  // Case_I6 (P red && U black && N outer grandchild of G):
  RotateDirRoot(T,G,1-dir); // G may be the root
  P->color = BLACK;
  G->color = RED;
  return; // insertion complete
} // end of RBinsert1

Mivel az algoritmus segédadatstruktúra használata nélkül átalakítja a bemenetet, és csak kis mennyiségű extra tárhelyet használ a segédváltozók számára, a helyén van .

Eltávolítás: egyszerű esetek

Az N címke az aktuális csomópontot jelöli, amely belépéskor a törlendő csomópont.

Ha N az a gyökér, amely nem rendelkezik nem NIL gyermekkel, akkor egy NIL csomópont váltja fel, ami után a fa üres-és RB alakú.

Ha N- nek két nem NIL gyermeke van, akkor egy további navigáció vagy a bal alfa maximális eleméhez (amely a sorrendben elődje), vagy a jobb alfa minimális eleméhez (amely a rendezett utód) talál egy csomópontot nincs más csomópont között ( itt látható ). Anélkül, hogy megérintené a csomópont felhasználói adatait, a csomópont és az N összes piros-fekete fa mutatója kicserélődik, így N- nek legfeljebb egy nem NIL gyermeke van.

Ha N- nek pontosan egy nem NIL gyermeke van, akkor annak vörösnek kell lennie, mert ha fekete lenne, akkor a 4. követelmény egy második fekete nem NIL gyermeket kényszerítene.

Ha N egy piros csomópont, akkor nem lehet nem NIL gyermeke, mert ennek a 3. követelmény szerint fekete színűnek kell lennie . Ezenkívül nem lehet pontosan egy fekete gyermeke, amint azt fentebb vitattuk. Ennek eredményeként a piros N csomópont gyermektelen, és egyszerűen eltávolítható.

Ha N fekete csomópont, akkor lehet, hogy vörös gyermeke van, vagy egyáltalán nincs nem NIL gyermeke. Ha N -nek vörös gyermeke van, akkor ezt a gyermeket egyszerűen lecserélik, miután az utóbbit feketére festették.

Fekete, nem gyökérlevél eltávolítása

A bonyolult eset az, amikor N nem a gyökér, fekete színű, és csak NIL gyermeke van (⇔ nincs megfelelő gyermek). Az első iterációban N helyébe NIL lép.

void RBdelete2(
  RBtree* T,         // -> red–black tree
  struct RBnode* N)  // -> node to be deleted
 {
  struct RBnode* P = N->parent;  // -> parent node of N
  byte dir;          // side of P on which N is located (∈ { LEFT, RIGHT })
  struct RBnode* S;  // -> sibling of N
  struct RBnode* C;  // -> close   nephew
  struct RBnode* D;  // -> distant nephew

  // P != NULL, since N is not the root.
  dir = childDir(N); // side of parent P on which the node N is located
  // Replace N at its parent P by NIL:
  P->child[dir] = NIL;
  goto Start_D;      // jump into the loop

  // start of the (do while)-loop:
  do {
    dir = childDir(N);   // side of parent P on which node N is located
Start_D:
    S = P->child[1-dir]; // sibling of N (has black height >= 1)
    D = S->child[1-dir]; // distant nephew
    C = S->child[  dir]; // close   nephew
    if (S->color == RED)
      goto Case_D3;                  // S red ===> P+C+D black
    // S is black:
    if (D != NIL && D->color == RED) // not considered black
      goto Case_D6;                  // D red && S black
    if (C != NIL && C->color == RED) // not considered black
      goto Case_D5;                  // C red && S+D black
    // Here both nephews are == NIL (first iteration) or black (later).
    if (P->color == RED)
      goto Case_D4;                  // P red && C+S+D black

Az egyensúlyozó hurok a következő változatlan :

• Minden iteráció elején N fekete magassága megegyezik az iterációs számmal, mínusz eggyel, ami azt jelenti, hogy az első iterációban nulla, és hogy N egy igazi fekete csomópont magasabb iterációkban.
• A fekete csomópontok száma az N-n keresztül vezető utakon eggyel kevesebb, mint a törlés előtt, míg az összes többi útvonalon változatlan, így P - nél fekete sértés van , ha vannak más utak.
• Az összes többi tulajdonság (beleértve a 3. követelményt is ) teljes egészében teljesül.

Megjegyzések a diagramok törléséhez

előtt

eset →

forgatóberende- CIÓ

assig- nment

után

→ következő

Δh

P

C

S

D

P

C

S

D

-

D2

→

D3

P ↶ S

N : = N

?

?

?

0

D1

N : = P

?

?

1

D4

→

D5

C ↷ S

N : = N

D6

0

D6

P ↶ S

→

Törlés: Ez a szinopszis az előző oszlopban azt mutatja, hogy a színcsillagok minden                 lehetséges esete le van fedve.

• Az alábbi diagramok, P használják N „s szülő, S a testvére N , C (azaz közel unokaöccse) az S „s gyermek ugyanabba az irányba, mint N , és a D (azaz távoli unokaöccse) az S „s másik gyermek ( S nem lehet NIL csomópont az első iterációban, mert az első fekete magassággal kell rendelkeznie, ami a törlés előtt N fekete magassága volt , de C és D lehet NIL csomópont).
• A diagramok az aktuális N csomópontot a szülő P bal gyermekeként mutatják, annak ellenére, hogy N mindkét oldalon lehet. A kódminták mindkét lehetőséget lefedik az oldalsó változó segítségével dir.
• Az eltávolítás elején (az első iterációban) N a törlendő csomópontot helyettesítő NIL csomópont. Mivel a szülői csomópontban való elhelyezkedése az egyetlen fontos dolog, ezt a szimbólum jelzi (jelentése: az aktuális N csomópont NIL csomópont és bal oldali gyermek) a törlési diagramok bal oszlopában. A művelet előrehaladtával a megfelelő (fekete magasságú ≥ 1) csomópontok is áram alá kerülhetnek (lásd pl . D1 eset ).
• A törlési diagramban a fekete golyókat ( és ) megszámolva megfigyelhető, hogy az N -n keresztül vezető utak egy golyóval kevesebbek, mint a többi út. Ez fekete szabálysértést jelent P-nél- ha létezik.
• A szín konstelláció oszlop csoport előtt határozza meg a helyzet, akinek a neve oszlopban megadott ügyben . Ezáltal az üresen hagyott cellák lehetséges értékeit figyelmen kívül hagyja.
• A szinopszis sorai úgy vannak elrendezve, hogy az összes lehetséges RB eset lefedettsége könnyen érthető legyen.
• Az oszlopot forgatás jelzi, hogy a forgatás hozzájárul a kiegyensúlyozás.
• Az oszlop hozzárendelése N hozzárendelést mutat, mielőtt belép egy következő lépésbe. Ez valószínűleg a többi P , C , S , D csomópont átrendelését is indukálja .
• Ha valami megváltozott a helyzet, ezt mutatja az oszlop csoport után .
• A nyíl → a következő oszlopban azt jelzi, hogy ezzel a lépéssel befejeződött az újraegyensúlyozás. Ha az utólagos oszlop pontosan egy esetet határoz meg, akkor ezt az esetet adjuk meg következőként, különben kérdőjelek vannak.
• A hurok tartalmazza a metszeteken Start_Dkeresztül „Törlés esetén 1” , ha a probléma a kiegyensúlyozás emeljük szinttel feljebb a fa, hogy a szülő P lesz az új aktuális csomópont N . Tehát a fa (hol van a fa magassága) javítása maximális iterációt igényel . Mivel az eszkaláció valószínűsége exponenciálisan csökken minden iterációval, a teljes újraegyensúlyozási költség átlagosan állandó, de amortizált állandó . (Csak mellesleg: Mehlhorn & Sanders rámutat: "Az AVL fák nem támogatják az állandó amortizált frissítési költségeket." Ez igaz a törlés utáni egyensúlyra, de nem az AVL beillesztésre.)${\ displaystyle \ Delta h = 1}$${\ displaystyle h}$${\ displaystyle h}$
• A hurok testéből kilépő ágak vannak a D3 , D6 , D5 + D6 , D4 és D2 esetekhez ; a "3. eset törlése" szekciónak három különböző kimenő ága van a D6 , D5 és D4 esetekhez .
• A D6 és D5 + D6 és D3 + D5 + D6 esetekben fordulások fordulnak elő - mindez a hurkon kívül. Ezért összesen legfeljebb három forgatás fordul elő.

→ Szimbólumok magyarázata

első iteráció

nagyobb iteráció

1. eset törlése

1. eset törlése

P , S és S gyermekei feketék. Festés után S piros összes áthalad S , amelyek pontosan azok útvonalakat nem halad át N , eggyel kevesebb fekete csomópontot. Most a P által gyökerezett alfa minden útján azonos számú fekete csomópont van, de eggyel kevesebb, mint azok az utak, amelyek nem haladnak át a P -n , így a 4. követelmény még mindig megsérthető. Miután újra- címkézésekor P , hogy N a hurok invariáns teljesül, hogy a kiegyensúlyozás iterálhatók egy fekete szint (= 1 fa szintjén) magasabb.

    // Case_D1 (P+C+S+D black):
    S->color = RED;
    N = P; // new current node (maybe the root)
    // iterate 1 black level
    //   (= 1 tree level) higher
  } while ((P = N->parent) != NULL);
  // end of the (do while)-loop

2. eset törlése

Az aktuális N csomópont az új gyökér. Egy fekete csomópontot eltávolítottak minden útból, így az RB tulajdonságok megmaradnak. A fa fekete magassága 1 -gyel csökken.

  // Case_D2 (P == NULL):
  return; // deletion complete

első iteráció

nagyobb iteráció

Törölje az esetet 3

Törölje az esetet 3

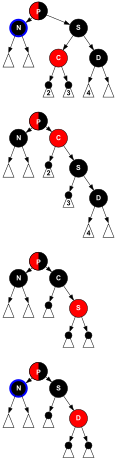
Az S testvér vörös, így P -nek és C és D unokaöccsének feketenek kell lennie. Egy dir-rotation a P fordul S be N „s nagyszülő. Ezután a P és S színek megfordítása után az N -n keresztül vezető út még mindig rövid, egy fekete csomópont. De N- nek van egy piros szülője P és egy fekete testvére S , így a D4, D5 vagy D6 esetek transzformációi képesek visszaállítani az RB alakot.

Case_D3: // S red && P+C+D black:
  RotateDirRoot(T,P,dir); // P may be the root
  P->color = RED;
  S->color = BLACK;
  S = C; // != NIL
  // now: P red && S black
  D = S->child[1-dir]; // distant nephew
  if (D != NIL && D->color == RED)
    goto Case_D6;      // D red && S black
  C = S->child[  dir]; // close   nephew
  if (C != NIL && C->color == RED)
    goto Case_D5;      // C red && S+D black
  // Otherwise C+D considered black.
  // fall through to Case_D4

első iteráció

nagyobb iteráció

4. eset törlése

4. eset törlése

A testvér S és S gyermekei feketék, de P vörös. Az S és P színeinek cseréje nem befolyásolja az S -n áthaladó utakon lévő fekete csomópontok számát , de egyet hozzáad az N -en keresztül vezető utakon lévő fekete csomópontok számához, pótolva a törölt fekete csomópontot ezeken az utakon.

Case_D4: // P red && S+C+D black:
  S->color = RED;
  P->color = BLACK;
  return; // deletion complete

első iteráció

nagyobb iteráció

5. eset törlése

5. eset törlése

Az S testvér fekete, S közeli gyermeke C vörös, S távoli gyermeke D fekete. Miután egy (1-dir)-rotation át S unokaöccse C válik S „s szülő és N „s új testvér. Az S és C színek felcserélődnek. Minden ösvényen még mindig ugyanannyi fekete csomópont található, de most N -nek van egy fekete testvére, akinek távoli gyermeke vörös, így a csillagkép alkalmas a D6 esetre. Sem N, sem szülő P nem érinti ezt az átalakítást, és P lehet piros vagy fekete ( az ábrán).

Case_D5: // C red && S+D black:
  RotateDir(S,1-dir); // S is never the root
  S->color = RED;
  C->color = BLACK;
  D = S;
  S = C;
  // now: D red && S black
  // fall through to Case_D6

első iteráció

nagyobb iteráció

6. eset törlése

6. eset törlése

Az S testvér fekete, S távoli gyermeke D vörös. Miután egy dir-rotation át P a testvér S válik a szülő a P és S „s távoli gyermek D . A P és az S színeket kicserélik, és a D feketévé válik. A részfa gyökerében még mindig ugyanaz a szín található, nevezetesen vörös vagy fekete ( az ábrán), amely ugyanarra a színre utal mind az átalakítás előtt, mind azt követően. Így a 3. követelmény megmarad. A részfában az N -n nem haladó utak (azaz a D -n és a 3. csomóponton áthaladnak az ábrán) ugyanannyi fekete csomóponton haladnak keresztül, mint korábban, de N -nek van egy további fekete őse: vagy P fekete lett, vagy fekete és S került hozzá fekete nagyszülőként. Így az N-en áthaladó utak egy további fekete csomóponton haladnak át, így a 4. követelmény helyreáll, és a teljes fa RB alakú.

Case_D6: // D red && S black:
  RotateDirRoot(T,P,dir); // P may be the root
  S->color = P->color;
  P->color = BLACK;
  D->color = BLACK;
  return; // deletion complete
} // end of RBdelete2

Mivel az algoritmus segédadatstruktúra használata nélkül átalakítja a bemenetet, és csak kis mennyiségű extra tárhelyet használ a segédváltozók számára, a helyén van .

A határok igazolása

4. ábra: Piros -fekete fák RB _h magasságú h = 1,2,3,4,5,
mindegyik minimális számmal 1,2,4,6 ill. 10 csomópont.

Mert van egy piros-fekete fa magassága és ${\ displaystyle h \ in \ mathbb {N}}$${\ displaystyle h}$

${\ displaystyle m_ {h}: = 2^{\ lfloor (h+1)/2 \ rfloor} +2^{\ lfloor h/2 \ rfloor} -2}$   csomópontok

és nincs ilyen magas vörös -fekete fa, kevesebb csomóponttal - ezért minimális .
Fekete magassága  ${\ displaystyle \ lfloor h/2 \ rfloor.}$

Bizonyíték

Ahhoz, hogy egy bizonyos magasságú vörös -fekete fa minimális számú csomóponttal rendelkezzen, pontosan egy leghosszabb útvonalnak kell lennie, maximális számú piros csomóponttal, hogy minimális fekete magassággal maximális fa magasságot érjen el. Ezen az útvonalon kívül minden más csomópontnak feketének kell lennie. Ha egy csomópontot eltávolítunk erről a fáról, akkor vagy elveszíti a magasságát, vagy valamilyen RB tulajdonságot.

A vörös gyökérrel rendelkező RB fa minimális. Ez egyetért ezzel ${\ displaystyle h = 1}$

${\ displaystyle m_ {1} = 2^{\ lfloor (1+1)/2 \ rfloor} \!+\! 2^{\ lfloor 1/2 \ rfloor} \! \!-\! \! 2 = 2^{1} \!+\! 2^{0} \! \!-\! \! 2 = 1 ~.}$

Egy minimális RB fa (RB _h a 4. ábrán) magassága gyökér, amelynek két gyermekrészfa különböző magasságú. A magasabb gyermek részfa szintén egy minimális RB fa, RB _{h –1} , amely szintén a leghosszabb utat tartalmazza , amely meghatározza a magasságát ; azt a csomópontok és a fekete magasság A másik részfájának egy tökéletes bináris fa a (fekete) magassága , amelynek fekete csomópontok-, és nincs piros pont. Ekkor a csomópontok száma indukcióval történik${\ displaystyle h> 1}$${\ displaystyle h \! \!-\! \! 1}$${\ displaystyle m_ {h-1}}$${\ displaystyle \ lfloor (h \! \!-\! \! 1)/2 \ rfloor =: s.}$${\ displaystyle s}$${\ displaystyle 2^{s} \! \!-\! \! 1 = 2^{\ lfloor (h-1)/2 \ rfloor} \! \!-\! \! 1}$

	${\ displaystyle m_ {h}}$	${\ displaystyle =}$	${\ displaystyle (m_ {h-1})}$	${\ displaystyle +}$	${\ displaystyle (1)}$	${\ displaystyle +}$	${\ displaystyle (2^{\ lfloor (h-1)/2 \ rfloor} -1)}$
			(magasabb részfa)		(gyökér)		(második részfa)
eredményezve
	${\ displaystyle m_ {h}}$	${\ displaystyle =}$	${\ displaystyle (2^{\ lfloor h/2 \ rfloor} +2^{\ lfloor (h-1)/2 \ rfloor} -2)}$	${\ displaystyle +}$	${\ displaystyle 2^{\ lfloor (h-1)/2 \ rfloor}}$
		${\ displaystyle =}$	${\ displaystyle 2^{\ lfloor h/2 \ rfloor} +2^{\ lfloor (h+1)/2 \ rfloor} -2}$. ■

A grafikon a függvény van konvex és szakaszosan lineáris töréspontokat át , ahol a funkciót táblázatba, mint A027383 ( h -1) a (szekvencia A027383 a OEIS-ben ).${\ displaystyle m_ {h}}$${\ displaystyle (h = 2k \; | \; m_ {2k} = 2 \ cdot 2^{k} \!-\! 2)}$${\ displaystyle k \ in \ mathbb {N}.}$${\ displaystyle m_ {h} =}$${\ displaystyle h \ geq 1}$

A függvény megoldása ${\ displaystyle h}$

Az egyenlőtlenség odáig vezet , furcsa módon ahhoz ${\ displaystyle 9> 8 = 2^{3}}$${\ displaystyle 3> 2^{3/2}}$${\ displaystyle h}$

${\ displaystyle m_ {h} = 2^{(h+1)/2} +2^{(h-1)/2} -2 = 3 \ cdot 2^{(h-1)/2} -2 = {\ bigl (} 3 \ cdot 2^{-3/2} {\ bigr)} \ cdot 2^{(h+2)/2} -2> 2 \ cdot 2^{h/2} -2 ,}$,

ami hoz

${\ displaystyle m_ {h} \ geq 2 \ cdot 2^{h/2} -2}$

mindenkinek (páratlan és páratlan). Így van ez az intervallumban is ${\ displaystyle h}$${\ displaystyle h}$

	${\ displaystyle \ log _ {2} (n+1)}$	${\ displaystyle \ leq h \ leq}$	${\ displaystyle 2 \ log _ {2} (n+2) -2 = 2 \ log _ {2} (n/2+1)}$	${\ displaystyle {\ bigl [} <2 \ log _ {2} (n+1) \; {\ bigr]}}$
	(tökéletes bináris fa)		(minimális piros -fekete fa)

azzal , hogy a csomópontok száma. ${\ displaystyle n}$

Következtetés

A piros -fekete fa csomópontokkal (kulcsokkal) magassága van${\ displaystyle n}$${\ displaystyle h \ in {\ mathcal {O}} (\ log n).}$

Műveletek és tömeges műveletek beállítása

Az egy elemből álló beszúrási, törlési és keresési műveleteken kívül számos halmazműveletet definiáltak a vörös-fekete fákon: egyesítés , metszéspont és halmazkülönbség . Ekkor a beillesztések vagy törlések gyors tömeges műveletei valósíthatók meg ezen beállítási funkciók alapján. Ezek a beállított műveletek támaszkodhat két segítő műveletek Osztott és be . Az új műveletek révén a vörös-fekete fák megvalósítása hatékonyabb és párhuzamosabb lehet. Ez a megvalósítás lehetővé teszi a vörös gyökeret.

• Csatlakozás : A Csatlakozás függvény két piros -fekete fán t ₁ és t ₂ és egy k kulcson található , ahol t ₁ < k < t ₂ , azaz minden t ₁ -es billentyű kisebb, mint k , és minden t ₂ -es billentyű nagyobb mint k . Visszaad egy fát, amely tartalmazza a t ₁ , t ₂ , valamint a k összes elemét .

Ha a két fa egyforma fekete magasságú, akkor a Join egyszerűen létrehoz egy új csomópontot a bal oldali t ₁ , k gyökérrel és a t ₂ jobb alfával . Ha mind a t _1, mind a t ₂ fekete gyökerű, állítsa a k értéket pirosra. Ellenkező esetben k feketére van állítva.

Ha a fekete magasságok egyenlőtlenek, tegyük fel, hogy t ₁ nagyobb fekete magasságú, mint t ₂ (a másik eset szimmetrikus). Csatlakozás követi a t ₁ jobb gerincét, amíg egy fekete c csomópont van , amely kiegyensúlyozott a t _{2 -vel} . Ezen a ponton egy új csomópont jön létre, amely bal c gyermeket , k gyökeret (pirosra állítva) és jobb t ₂ utódot hoz létre a c helyett. Az új csomópont érvénytelenítheti a piros -fekete változatot, mert legfeljebb három piros csomópont jelenhet meg egy sorban. Ez dupla forgatással rögzíthető. Ha a kettős piros probléma a gyökérhez terjed, akkor a gyökér fekete lesz, és visszaállítja a tulajdonságokat. Ennek a funkciónak a költsége a két bemeneti fa közötti fekete magasságok különbsége.

• Osztott : felosztásához piros-fekete fa két kisebb fák, azok kisebb kulcsot x , és azok nagyobb kulcsot x először dolgozzon az utat a gyökér behelyezésével x a piros-fekete fa. A beszúrás után minden x -nél kisebb érték megtalálható az útvonal bal oldalán, és minden x -nél nagyobb érték a jobb oldalon. A Csatlakozás alkalmazásával a bal oldali összes részfa alulról felfelé összevonásra kerül az útvonal billentyűivel, köztes csomópontokként alulról felfelé a bal oldali fa létrehozásához, és a jobb rész szimmetrikus.

Bizonyos alkalmazásoknál a Split logikai értéket is visszaad, amely jelzi, ha x megjelenik a fában. Az ára osztott a sorrendben a fa magasságát. Ennek az algoritmusnak valójában semmi köze a vörös -fekete fa különleges tulajdonságaihoz, és minden olyan fán használható, amelyhez kapcsolódási művelet tartozik, például AVL -fához .${\ displaystyle {\ mathcal {O}} (\ log n),}$

A csatlakozási algoritmus a következő:

function joinRightRB(TL, k, TR)
    if r(TL)=⌊r(TL)/2⌋×2:
        return Node(TL,⟨k,red⟩,TR)
    else 
        (L',⟨k',c'⟩,R')=expose(TL)
        T'=Node(L',⟨k',c'⟩,joinRightRB(R',k,TR)
        if (c'=black) and (T'.right.color=T'.right.right.color=red):
            T'.right.right.color=black;
            return rotateLeft(T')
        else return T'

function joinLeftRB(TL, k, TR)
  /* symmetric to joinRightRB */

function join(TL, k, TR)
    if ⌊r(TL)/2⌋>⌊r(TR)/2⌋×2:
        T'=joinRightRB(TL,k,TR)
        if (T'.color=red) and (T'.right.color=red):
            T'.color=black
        return T'
    else if ⌊r(TR)/2⌋>⌊r(TL)/2⌋×2
        /* symmetric */
    else if (TL.color=black) and (TR.color=black)
        Node(TL,⟨k,red⟩,TR)
    else
        Node(TL,⟨k,black⟩,TR)

Itt egy csomópont a fekete csomópont fekete magasságának kétszeresét, a piros csomópont fekete magasságának kétszerese. expose (v) = (l, ⟨k, c⟩, r) azt jelenti, hogy kivonjuk a facsomópont bal gyermekét , a csomópont kulcsát, a csomópont színét és a jobb utódot . A csomópont (l, ⟨k, c⟩, r) azt jelenti, hogy bal csomópontot hozzon létre bal gyermekből , kulcsból , színből és jobb gyermekből . ${\ displaystyle r (v)}$${\ displaystyle v}$${\ displaystyle v}$${\ displaystyle l}$${\ displaystyle k}$${\ displaystyle c}$${\ displaystyle r}$${\ displaystyle l}$${\ displaystyle k}$${\ displaystyle c}$${\ displaystyle r}$

A felosztási algoritmus a következő:

function split(T, k)
    if (T = nil) return (nil, false, nil)
    (L,(m,c),R) = expose(T)
    if (k = m) return (L, true, R)
    if (k < m) 
        (L',b,R') = split(L, k)
        return (L',b,join(R',m,R))
    if (k>m) 
        (L',b,R') = split(R, k)
        return (join(L,m,L'),b,R))

A unió két piros-fekete fák t ₁ és t ₂ képviselő készlet A és B , egy piros-fekete fa t , amely képviseli A ∪ B . A következő rekurzív függvény számítja ki ezt az uniót:

function union(t1, t2):
    if t1 = nil:
        return t2
    if t2 = nil:
        return t1
    t<, t> ← split t2 on t1.root
    return join(t1.root, union(left(t1), t<), union(right(t1), t>))

Ebben az esetben a split két fát ad vissza: az egyik a billentyűket, a beviteli billentyűt kevésbé, a másik pedig a nagyobb billentyűket. (Az algoritmus roncsolásmentes , de létezik helyben romboló verzió is.)

A metszés vagy eltérés algoritmusa hasonló, de megköveteli a Join2 segédprogramot, amely megegyezik a Csatlakozással, de a középső kulcs nélkül. Az egyesítés, metszéspont vagy eltérés új funkciói alapján egy vagy több kulcs is beilleszthető a piros -fekete fába, vagy törölhető belőle. Mivel a felosztás hívja a Csatlakozást, de nem foglalkozik közvetlenül a vörös-fekete fák kiegyensúlyozási kritériumaival, az ilyen megvalósítást általában "csatlakozási alapú" megvalósításnak nevezik .

Az egyesülés, metszéspont és eltérés összetettsége két piros -fekete fa méretű és . Ez az összetettség az összehasonlítások számát tekintve optimális. Ennél is fontosabb, mivel a rekurzív hívások unió, metszet vagy különbség függetlenek egymástól, akkor lehet végrehajtani párhuzamosan egy párhuzamos mélységben . Amikor az összekapcsolás-alapú megvalósítás ugyanazzal a számítással irányított aciklikus gráffal (DAG) rendelkezik, mint az egyelemes beszúrás és törlés, ha a nagyobb fa gyökerét használják a kisebb fa felosztásához. ${\ displaystyle {\ mathcal {O}} (\ bal (m \ log \ left ({n \ over m} +1 \ right) \ right)}$${\ displaystyle m}$${\ displaystyle n (\ geq m)}$ ${\ displaystyle {\ mathcal {O}} (\ log m \ log n)}$${\ displaystyle m = 1}$

Párhuzamos algoritmusok

A párhuzamos algoritmusok a vörös -fekete fák felépítéséhez az elemek rendezett listáiból a számítógép típusától függően állandó időben vagy időben futhatnak , ha a rendelkezésre álló processzorok száma aszimptotikusan arányos az elemek számával . A gyors keresés, beillesztés és törlés párhuzamos algoritmusok is ismertek. ${\ displaystyle {\ mathcal {O}} (\ log \ log n)}$${\ displaystyle n}$${\ displaystyle n \ to \ infty}$

A piros-fekete fák összekapcsolási alapú algoritmusai párhuzamosak a tömeges műveletekhez, beleértve az egyesítést, metszést, építést, szűrést, térképcsökkentést stb.

Párhuzamos tömeges műveletek

Az olyan alapvető műveletek, mint a beillesztés, eltávolítás vagy frissítés párhuzamosíthatók, ha meghatározzák a több elemből álló tömegeket feldolgozó műveleteket. Lehetőség van a tömegek feldolgozására több alapvető művelettel is, például a tömegek tartalmazhatnak beillesztendő elemeket és a fából eltávolítandó elemeket.

Az ömlesztett műveletek algoritmusai nem csak a piros-fekete fára alkalmazhatók, hanem más rendezett szekvenciaadat-struktúrákhoz is alkalmazhatók, például a 2–3 , 2–3–4 fa és (a, b)- fa . A következőkben a tömeges beszúrás különböző algoritmusait ismertetjük, de ugyanezek az algoritmusok alkalmazhatók az eltávolításra és a frissítésre is. A tömeges beszúrás olyan művelet, amely a sorozat minden elemét beilleszti a fába . ${\ displaystyle I}$${\ displaystyle T}$

Csatlakozás alapú

Ez a megközelítés alkalmazható minden rendezett szekvencia adatstruktúrára, amely támogatja a hatékony összekapcsolási és felosztási műveleteket. Az általános elképzelés az, hogy feldaraboljuk és több részre osztjuk, és párhuzamosan hajtjuk végre a behelyezéseket ezeken a részeken. ${\ displaystyle I}$${\ displaystyle T}$

1. Először a beillesztendő elemek nagy részét kell rendezni.${\ displaystyle I}$
2. Ezt követően, az algoritmus osztja be részein körülbelül azonos méretű.${\ displaystyle I}$${\ displaystyle k \ in \ mathbb {N} ^{+}}$${\ displaystyle \ langle I_ {1}, \ cdots, I_ {k} \ rangle}$
3. Ezután a fa kell lennie osztott részeit oly módon, hogy a minden következő korlátozások érvényesek: ${\ displaystyle T}$${\ displaystyle k}$${\ displaystyle \ langle T_ {1}, \ cdots, T_ {k} \ rangle}$${\ displaystyle j \ in \ mathbb {N} ^{+} | \, 1 \ leq j <k}$
   1. ${\ displaystyle {\ text {last}} (I_ {j}) <{\ text {first}} (T_ {j+1})}$
   2. ${\ displaystyle {\ text {last}} (T_ {j}) <{\ text {first}} (I_ {j+1})}$
4. Most az algoritmus beilleszt minden elemét figyelembe egymást. Ezt a lépést mindenki számára végre kell hajtani , amit párhuzamosan akár a processzorok is elvégezhetnek .${\ displaystyle I_ {j}}$${\ displaystyle T_ {j}}$${\ displaystyle j}$${\ displaystyle k}$
5. Végül a kapott fákat összekapcsolják, hogy az egész művelet végeredményét képezzék.

Vegye figyelembe, hogy a 3. lépésben a felosztási korlátozások biztosítják, hogy az 5. lépésben a fák újra összekapcsolhatók, és a kapott sorrend rendezésre kerüljön. ${\ displaystyle I}$

• 

  kezdeti fa

• 

  én és T felosztása

• 

  illessze be a hasított T -be

• 

  közös

Az álkód a tömeges beillesztés illesztési alapú algoritmusának egyszerű osztás és meghódítása megvalósítását mutatja. Mindkét rekurzív hívás párhuzamosan hajtható végre. Az itt használt összekapcsolási művelet eltér az ebben a cikkben kifejtett verziótól, helyette a join2 -t használjuk, amely kimarad a második k paraméterből.

bulkInsert(T, I, k):
    I.sort()
    bulklInsertRec(T, I, k)

bulkInsertRec(T, I, k):
    if k = 1:
        forall e in I: T.insert(e)
    else
        m := ⌊size(I) / 2⌋
        (T1, _, T2) := split(T, I[m])
        bulkInsertRec(T1, I[0 .. m], ⌈k / 2⌉)
            || bulkInsertRec(T2, I[m + 1 .. size(I) - 1], ⌊k / 2⌋)
        T ← join2(T1, T2)

Végrehajtási idő

A rendezést ebben az elemzésben nem veszik figyelembe. ${\ displaystyle I}$

#rekurziós szintek	${\ displaystyle \ in {\ mathcal {O}} (\ log k)}$
T (felosztás) + T (csatlakozás)	${\ displaystyle \ itt: {\ mathcal {O}} (\ log | T |)}$
behelyezések szálonként	${\ displaystyle \ itt: {\ mathcal {O}} \ bal ({\ frac {| I |} {k}} \ jobb)}$
T (beillesztés)	${\ displaystyle \ itt: {\ mathcal {O}} (\ log | T |)}$
T (bulkInsert) = = processzorokkal${\ displaystyle k}$	${\ displaystyle \ itt: {\ mathcal {O}} \ bal (\ log k \ log | T |+{\ frac {| I |} {k}} \ log | T | \ right)}$

Ez javítható párhuzamos algoritmusok használatával a felosztáshoz és összekapcsoláshoz. Ebben az esetben a végrehajtási idő . ${\ displaystyle \ in {\ mathcal {O}} \ bal (\ log | T |+{\ frac {| I |} {k}} \ log | T | \ right)}$

Munka

#hasad, #csatlakozik	${\ displaystyle \ in {\ mathcal {O}} (k)}$
W (felosztás) + W (csatlakozás)	${\ displaystyle \ itt: {\ mathcal {O}} (\ log | T |)}$
#beillesztések	${\ displaystyle \ in {\ mathcal {O}} (| I |)}$
W (beillesztés)	${\ displaystyle \ itt: {\ mathcal {O}} (\ log | T |)}$
W (tömeges beszúrás)	${\ displaystyle \ in {\ mathcal {O}} (k \ log | T |+| I | \ log | T |)}$

Csővezeték

A tömeges műveletek párhuzamosításának másik módja a csővezetéki megközelítés alkalmazása. Ezt úgy tehetjük meg, hogy az alapművelet feldolgozásának feladatát részfeladatok sorozatára bontjuk. Több alapművelet esetén az alfeladatok párhuzamosan feldolgozhatók úgy, hogy minden egyes részfeladatot külön processzorhoz rendelnek.

1. Először a beillesztendő elemek nagy részét kell rendezni.${\ displaystyle I}$
2. Az algoritmus minden eleméhez megtalálja a megfelelő beillesztési pozíciót . Ez párhuzamosan megtehető minden elem esetében, mivel ebben a folyamatban nem mutálódik. Most az egyes elemek beillesztési helyzetének megfelelően alsorozatokra kell osztani . Például az alsorozat tartalmazza azokat az elemeket, amelyek beszúrási pozíciója a csomóponttól balra lenne .${\ displaystyle I}$${\ displaystyle T}$${\ displaystyle \ itt: I}$${\ displaystyle T}$${\ displaystyle I}$${\ displaystyle S}$${\ displaystyle s_ {n, {\ mathit {left}}}}$${\ displaystyle I}$${\ displaystyle n}$
3. A középső elem minden részsorozat lesz beillesztve , mint egy új csomópont . Ez párhuzamosan végezhető mindegyiknél, mivel definíciójuk szerint mindegyik beillesztési pozíciója egyedi. Ha balra vagy jobbra tartalmaz elemeket , akkor ezek egy új alsorozatba kerülnek, mint vagy .${\ displaystyle m_ {n, {\ mathit {dir}}}}$${\ displaystyle s_ {n, {\ mathit {dir}}}}$${\ displaystyle T}$${\ displaystyle n '}$${\ displaystyle m_ {n, {\ mathit {dir}}}}$${\ displaystyle m_ {n, {\ mathit {dir}}}}$${\ displaystyle s_ {n, {\ mathit {dir}}}}$${\ displaystyle m_ {n, {\ mathit {dir}}}}$${\ displaystyle S}$${\ displaystyle s_ {n ', {\ mathit {left}}}}$${\ displaystyle s_ {n ', {\ mathit {right}}}}$
4. Most valószínűleg két egymást követő piros csomópontot tartalmaz az utak végén, amelyek a levelek gyökerét képezik, és amelyet javítani kell. Vegye figyelembe, hogy javítás közben az elemek beillesztési pozícióját frissíteni kell, ha a megfelelő csomópontokat befolyásolja a forgatás. Ha két csomópontnak különböző legközelebbi fekete őse van, akkor párhuzamosan javíthatók. Mivel legfeljebb négy csomópontnak lehet ugyanaz a legközelebbi fekete őse, a legalacsonyabb szinten lévő csomópontok állandó számú párhuzamos lépésben javíthatók. Ezt a lépést egymás után alkalmazzák a fenti fekete szintekre, amíg teljesen meg nem javul.${\ displaystyle T}$${\ displaystyle \ in S}$
   
   ${\ displaystyle T}$
5. A 3–5. Lépést meg kell ismételni az új alsorozatokon, amíg az üres nem lesz. Ezen a ponton minden elem beillesztésre került. Ezen lépések minden alkalmazását szakasznak nevezzük . Mivel az alsorozatok hossza az -ban van, és minden szakaszban az alsorozatok felére csökkennek, a szakaszok száma . Mivel minden szakasz felfelé halad a fa fekete szintjein, párhuzamosíthatók egy csővezetékben. Miután egy szakasz befejezte az egyik fekete szint feldolgozását, a következő szakasz képes feljebb lépni és ezen a szinten folytatni.${\ displaystyle S}$${\ displaystyle \ itt: I}$${\ displaystyle S}$${\ displaystyle \ in {\ mathcal {O}} (| I |)}$${\ displaystyle \ in {\ mathcal {O}} (\ log | I |)}$
   

• 

  Kezdeti fa

• 

  Keresse meg a betétpozíciókat

• 

  Az 1. szakasz elemeket illeszt be

• 

  Az 1. szakasz megkezdi a csomópontok javítását

• 

  A 2. szakasz elemeket illeszt be

• 

  A 2. szakasz megkezdi a csomópontok javítását

• 

  A 3. szakasz elemeket illeszt be

• 

  A 3. szakasz megkezdi a csomópontok javítását

• 

  A 3. szakasz folytatja a csomópontok javítását

Végrehajtási idő

A rendezést ebben az elemzésben nem veszik figyelembe. Ezenkívül feltételezzük, hogy kisebb, mint , különben hatékonyabb lenne a kapott fát a semmiből felépíteni. ${\ displaystyle I}$${\ displaystyle | I |}$${\ displaystyle | T |}$

T (keresse meg a betét pozícióját)	${\ displaystyle \ itt: {\ mathcal {O}} (\ log | T |)}$
#szakasz	${\ displaystyle \ in {\ mathcal {O}} (\ log | I |)}$
T (beillesztés) + T (javítás)	${\ displaystyle \ itt: {\ mathcal {O}} (\ log | T |)}$
T (bulkInsert) ~ #processzorokkal${\ displaystyle | I |}$	${\ displaystyle \ itt: {\ mathcal {O}} (\ log | I | +2 \ cdot \ log | T |)}$ ${\ displaystyle = {\ mathcal {O}} (\ log | T |)}$

Munka

W (keresse meg a betéthelyeket)	${\ displaystyle \ itt: {\ mathcal {O}} (| I | \ log | T |)}$
#beszúrások, #javítások	${\ displaystyle \ in {\ mathcal {O}} (| I |)}$
W (beillesztés) + W (javítás)	${\ displaystyle \ itt: {\ mathcal {O}} (\ log | T |)}$
W (tömeges beszúrás)	${\ displaystyle \ in {\ mathcal {O}} (2 \ cdot | I | \ log | T |)}$ ${\ displaystyle = {\ mathcal {O}} (| I | \ log | T |)}$

Népszerű kultúra

A vörös -fekete fára helyesen hivatkoztak a Missing egyik epizódjában, ahogy Robert Sedgewick megjegyezte egyik előadásában:

Jess : Megint a piros ajtó volt.
Pollock : Azt hittem, a piros ajtó a tárolóedény.
Jess : De már nem vörös volt, hanem fekete.
Antonio : Mit jelent tehát a vörös feketére váltás?
Pollock : Költségvetési hiány, piros tinta, fekete tinta.
Antonio : Ez egy bináris keresőfából származhat. A piros -fekete fa minden egyszerű útvonalat követ a csomóponttól a leszármazott levélig, amely azonos számú fekete csomóponttal rendelkezik.
Jess : Ez segít a hölgyekben?

Lásd még

• Az adatstruktúrák listája
• Fa adatszerkezet
• A fa forgása
• AA fa , a vörös -fekete fa egyik változata
• AVL fa
• B-fa ( 2–3 fa , 2–3–4 fa , B+ fa , B*fa , UB-fa )
• Scapegoat fa
• Spray fa
• T-fa
• WAVL fa

Hivatkozások és jegyzetek

További irodalom

• Mathworld: Piros -fekete fa
• San Diego Állami Egyetem: CS 660: Piros -fekete fajegyek, Roger Whitney
• Pfaff, Ben (2004. június). "A BST -k teljesítményelemzése a rendszerszoftverben" (PDF) . Stanford Egyetem .

Külső linkek

• Ben Pfaff: Bevezetés a bináris keresési fákba és a kiegyensúlyozott fákba. Free Software Foundation, Boston 2004, ftp.gnu.org (PDF gzip; 1662 kB)
• Vörös -fekete fa megvalósítás C -ban
• Teljes és működőképes megvalósítás C -ban
• OCW MIT előadás Prof. Erik Demaine -tól a vörös fekete fákon -
• Bináris keresési fa beillesztési vizualizáció a YouTube-on- Véletlenszerű és előre válogatott adatbeillesztések megjelenítése elemi bináris keresési fákban és balra dőlő piros-fekete fákban
• Egy tolakodó piros -fekete fa, C ++ nyelven írva
• Piros -fekete BST -k a 3.3 kiegyensúlyozott keresési fákban
• Piros -fekete BST Demo