Lineáris egyenletrendszer - System of linear equations

A matematika , egy lineáris egyenletrendszer (vagy lineáris rendszer ) van egy gyűjtemény egy vagy több lineáris egyenletek bevonásával ugyanazokat a változók . Például,

${\ displaystyle {\ begin {alignedat} {7} 3x && \;+\; && 2y && \;-\; && z && \; = \; && 1 & \\ 2x && \;-\; & 2y && \;+\; && 4z && \; = \ ; &&-2 & \\-x && \;+\; && {\ tfrac {1} {2}} y && \;-\; && z && \; = \; && 0 & end {alignedat}}}$

egy három egyenletből álló rendszer a három x , y , z változóban . A lineáris rendszer megoldása az értékek hozzárendelése a változókhoz úgy, hogy minden egyenlet egyszerre teljesül. A fenti rendszer megoldását a

${\ displaystyle {\ begin {alignedat} {2} x & \, = \, & 1 \\ y & \, = \, &-2 \\ z & \, = \, &-2 \ end {alignedat}}}$

mivel mindhárom egyenletet érvényesíti. A "rendszer" szó azt jelzi, hogy az egyenleteket együttesen, nem pedig egyénileg kell figyelembe venni.

A matematikában a lineáris rendszerek elmélete a lineáris algebra alapja és alapvető része , egy olyan tantárgy, amelyet a modern matematika legtöbb részében használnak. A megoldások megtalálására szolgáló számítási algoritmusok fontos részét képezik a numerikus lineáris algebrának , és kiemelkedő szerepet játszanak a mérnöki tudományban , a fizikában , a kémiában , az informatikában és a közgazdaságtanban . A nemlineáris egyenletek rendszerét gyakran közelíthetjük egy lineáris rendszerrel (lásd linearizáció ), amely hasznos módszer egy viszonylag összetett rendszer matematikai modelljének vagy számítógépes szimulációjának elkészítésekor .

Nagyon gyakran az egyenletek együtthatói valós vagy összetett számok, és a megoldásokat ugyanabban a számhalmazban keresik, de az elmélet és az algoritmusok bármely területen alkalmazhatók együtthatókra és megoldásokra . Mert mindezt egy integritástartomány mint a gyűrű az egész , vagy más algebrai struktúrák , más elméleteket fejlesztettek lásd lineáris egyenlet, mint egy gyűrű . Az egész számok lineáris programozása a "legjobb" egész megoldás megtalálásának módszereinek gyűjteménye (ha sok ilyen van). A Gröbner -báziselmélet algoritmusokat biztosít, ha az együtthatók és az ismeretlenek polinomok . A trópusi geometria is példa a lineáris algebrára egzotikusabb szerkezetben.

Elemi példák

Triviális példa

Egy egyenlet rendszere egy ismeretlenben

${\ displaystyle 2x = 4}$

megvan a megoldás

${\ displaystyle x = 2.}$

A lineáris rendszert azonban általában úgy tekintik, hogy legalább két egyenlete van.

Egyszerű, nem triviális példa

A legegyszerűbb nem triviális lineáris rendszer két egyenletet és két változót tartalmaz:

${\ displaystyle {\ begin {alignedat} {5} 2x && \;+\; && 3y && \; = \; && 6 & \\ 4x && \;+\; & 9y && \; = \; && 15 &. \ end {alignedat}}}$

Egy ilyen rendszer megoldásának egyik módja a következő. Először oldja meg a felső egyenletet a következők szerint : ${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle x = 3-{\ frac {3} {2}} y.}$

Most ezt a kifejezést x helyettesítse az alsó egyenletbe:

${\ displaystyle 4 \ left (3-{\ frac {3} {2}} y \ right)+9y = 15.}$

Ez egyetlen egyenletet eredményez, amely csak a változót tartalmazza . A megoldás megadja , és ezt visszahelyezzük a hozamok egyenletébe . Ez a módszer általánosan alkalmazható olyan rendszerekre, amelyek további változókkal rendelkeznek (lásd alább a "Változók kiküszöbölését", vagy az elemi algebráról szóló cikket .) ${\ displaystyle y}$${\ displaystyle y = 1}$${\ displaystyle x}$${\ displaystyle x = 3/2}$

Általános forma

Általános rendszere m lineáris egyenletek n ismeretlennel felírható

${\ displaystyle {\ begin {aligned} a_ {11} x_ {1}+a_ {12} x_ {2}+\ cdots+a_ {1n} x_ {n} & = b_ {1} \\ a_ {21} x_ {1}+a_ {22} x_ {2}+\ cdots+a_ {2n} x_ {n} & = b_ {2} \\ & \ \ \ vdots \\ a_ {m1} x_ {1}+a_ {m2} x_ {2} +\ cdots +a_ {mn} x_ {n} & = b_ {m}, \ end {aligned}}}$

hol vannak az ismeretlenek, ott vannak a rendszer együtthatói és az állandó kifejezések. ${\ displaystyle x_ {1}, x_ {2}, \ ldots, x_ {n}}$${\ displaystyle a_ {11}, a_ {12}, \ ldots, a_ {mn}}$${\ displaystyle b_ {1}, b_ {2}, \ ldots, b_ {m}}$

Gyakran az együtthatók és az ismeretlenek valós vagy összetett számok , de egész számok és racionális számok is láthatók, valamint polinomok és absztrakt algebrai szerkezet elemei .

Vektor egyenlet

Egy rendkívül hasznos véli, hogy minden ismeretlen a tömeg egy oszlopvektor egy lineáris kombinációja .

${\ displaystyle x_ {1} {\ begin {bmatrix} a_ {11} \\ a_ {21} \\\ vdots \\ a_ {m1} \ end {bmatrix}}+x_ {2} {\ begin {bmatrix} a_ {12} \\ a_ {22} \\\ vdots \\ a_ {m2} \ end {bmatrix}} +\ cdots +x_ {n} {\ begin {bmatrix} a_ {1n} \\ a_ {2n} \\\ vdots \\ a_ {mn} \ end {bmatrix}} = {\ begin {bmatrix} b_ {1} \\ b_ {2} \\\ vdots \\ b_ {m} \ end {bmatrix}}}$

Ez lehetővé teszi a vektoros terek (vagy általában modulok ) nyelvének és elméletének érvényesítését . Például, a gyűjtemény minden lehetséges lineáris kombinációival vektorok a bal oldali nevezzük a span , és az egyenletek egy megoldást csak akkor, amikor a jobb oldali vektor belül span. Ha ezen a tartományon belül minden vektornak pontosan egy kifejezése van a megadott bal oldali vektorok lineáris kombinációjaként, akkor minden megoldás egyedi. Mindenesetre a span egy alapot a lineárisan független vektorok csinálni garancia pontosan egy kifejezést; és ezen az alapon a vektorok száma ( mérete ) nem lehet nagyobb m -nél vagy n -nél , de lehet kisebb. Ez azért fontos, mert ha m független vektorunk van, a megoldás a jobb oldaltól függetlenül garantált, és egyébként nem garantált.

Mátrix egyenlet

A vektor egyenlet megegyezik a forma mátrix egyenletével

${\ displaystyle A \ mathbf {x} = \ mathbf {b}}$

ahol A egy m × n mátrix, X egy oszlopvektor a n bejegyzéseket, és b egy oszlop vektor m bejegyzéseket.

${\ displaystyle A = {\ begin {bmatrix} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & a_ {22} & \ cdots & a_ {2n} \\\ vdots & \ vdots & \ ddots & \ vdots \\ a_ {m1} & a_ {m2} & \ cdots & a_ {mn} \ end {bmatrix}}, \ quad \ mathbf {x} = {\ begin {bmatrix} x_ {1} \\ x_ {2} \\\ vdots \\ x_ {n} \ end {bmatrix}}, \ quad \ mathbf {b} = {\ begin {bmatrix} b_ {1} \\ b_ {2} \\\ vdots \ \ b_ {m} \ end {bmatrix}}}$

A vektorok számát a span alapon most a mátrix rangjaként fejezzük ki .

Megoldáskészlet

A lineáris rendszer megoldása az értékek hozzárendelése az x ₁ , x ₂ , ..., x _n változókhoz úgy, hogy minden egyenlet teljesül. A készlet az összes lehetséges megoldást az úgynevezett megoldás halmaz .

A lineáris rendszer a három lehetséges módszer bármelyikén viselkedhet:

1. A rendszernek végtelen sok megoldása van .
2. A rendszer egyetlen egyedi megoldást kínál .
3. A rendszernek nincs megoldása .

Geometriai értelmezés

Egy olyan rendszer, amely két változó ( x és y ), mindegyik lineáris egyenlet határozza meg egy vonalat a xy - síkon . Mivel egy lineáris rendszer megoldásának meg kell felelnie az összes egyenletnek, a megoldáshalmaz ezen egyenesek metszéspontja , tehát vagy egyenes, egyetlen pont vagy az üres halmaz .

Három változó, minden lineáris egyenlet határozza meg a síkot a háromdimenziós térben , és meghatározott megoldás a metszéspontja ezeket a gépeket. Így a megoldáshalmaz lehet sík, egyenes, egyetlen pont vagy üres halmaz. Például, mivel három párhuzamos síknak nincs közös pontja, egyenleteik megoldáshalmaza üres; egy pontban metsző három sík egyenleteinek megoldáshalmaza egyetlen pont; ha három sík halad át két ponton, egyenleteiknek legalább két közös megoldása van; valójában a megoldáshalmaz végtelen, és az összes pontot áthaladó egyenesből áll.

A n változók, minden lineáris egyenlet határozza meg a hipersík az n dimenziós térben . A megoldáshalmaz ezen hipersíkok metszéspontja, és lapos , amelynek bármely mérete n -nél kisebb lehet .

Általános viselkedés

Általában a lineáris rendszer viselkedését az egyenletek és az ismeretlenek száma közötti kapcsolat határozza meg. Itt az "általánosságban" azt jelenti, hogy az egyenletek együtthatóinak meghatározott értékeinél eltérő viselkedés léphet fel.

• Általánosságban elmondható, hogy egy ismeretlennél kevesebb egyenlettel rendelkező rendszer végtelen sok megoldást kínál, de lehet, hogy nincs megoldás. Az ilyen rendszert alul meghatározott rendszernek nevezik .
• Általában egy azonos számú egyenletet és ismeretlen rendszert tartalmazó rendszer egyetlen egyedi megoldással rendelkezik.
• Általánosságban elmondható, hogy az ismeretleneknél több egyenletet tartalmazó rendszerre nincs megoldás. Az ilyen rendszert túladagolt rendszernek is nevezik .

Az első esetben a megoldáshalmaz mérete általában n - m , ahol n a változók száma és m az egyenletek száma.

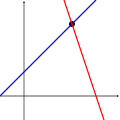
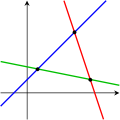
Az alábbi képek ezt a trichotómiát szemléltetik két változó esetén:

Egy egyenlet	Két egyenlet	Három egyenlet

Az első rendszer végtelen sok megoldást tartalmaz, nevezetesen a kék vonal összes pontját. A második rendszer egyetlen egyedi megoldást kínál, nevezetesen a két vonal metszéspontját. A harmadik rendszernek nincs megoldása, mivel a három vonalnak nincs közös pontja.

Nem szabad elfelejteni, hogy a fenti képek csak a leggyakoribb esetet (az általános esetet) mutatják. Lehetséges, hogy két egyenletből és két ismeretlenből álló rendszerben nincs megoldás (ha a két egyenes párhuzamos), vagy három egyenletből és két ismeretlenből álló rendszer megoldható (ha a három egyenes egyetlen pontban metszi egymást).

A lineáris egyenletrendszer az általános esettől eltérően viselkedik, ha az egyenletek lineárisan függenek , vagy ha következetlen, és nincs több egyenlete, mint ismeretlen.

Tulajdonságok

Függetlenség

Egy lineáris rendszer egyenletei függetlenek, ha egyik egyenlet sem vezethető le algebrai úton a többiekből. Ha az egyenletek függetlenek, minden egyenlet új információkat tartalmaz a változókról, és bármelyik egyenlet eltávolítása növeli a megoldáshalmaz méretét. A lineáris egyenletek esetében a logikai függetlenség megegyezik a lineáris függetlenséggel .

Például az egyenletek

${\ displaystyle 3x+2y = 6 \; \; \; \; {\ text {and}} \; \; \; \; 6x+4y = 12}$

nem függetlenek - ugyanaz az egyenlet, ha kettes tényezővel méretezik őket, és azonos gráfokat hoznának létre. Ez egy példa az egyenértékűségre egy lineáris egyenletrendszerben.

Egy bonyolultabb példa érdekében az egyenletek

${\ displaystyle {\ begin {alignedat} {5} x && \;-\; && 2y && \; = \; &&-1 & \\ 3x && \;+\; && 5y && \; = \; && 8 & \\ 4x && \;+\; && 3y && \; = \; && 7 & \ end {alignedat}}}$

nem függetlenek, mert a harmadik egyenlet a másik kettő összege. Valójában ezen egyenletek bármelyike ​​levezethető a másik kettőből, és bármelyik egyenlet eltávolítható anélkül, hogy befolyásolná a megoldáshalmazt. Ezen egyenletek grafikonjai három egyenes, amelyek egyetlen pontban metszik egymást.

Következetesség

A lineáris rendszer következetlen, ha nincs megoldása, és egyébként következetesnek mondják . Ha a rendszer inkonzisztens, akkor az egyenletekből ellentmondást lehet levonni, amely mindig átírható 0 = 1 állításként .

Például az egyenletek

${\ displaystyle 3x+2y = 6 \; \; \; \; {\ text {and}} \; \; \; \; 3x+2y = 12}$

következetlenek. Valójában, ha kivonjuk az első egyenletet a másodikból, és megszorozzuk az eredmény mindkét oldalát 1/6 -al, 0 = 1 -et kapunk . Ezen egyenletek grafikonjai az xy síkon párhuzamos egyenesek.

Lehetséges, hogy három lineáris egyenlet inkonzisztens, bár bármelyik kettő együtt is konzisztens. Például az egyenletek

${\ displaystyle {\ begin {alignedat} {7} x && \;+\; && y && \; = \; && 1 & \\ 2x && \;+\; && y && \; = \; && 1 & \\ 3x && \;+\; && 2y && \ ; = \; && 3 & \ end {alignedat}}}$

következetlenek. Az első két egyenletet összeadva 3 x + 2 y = 2 adódik , amelyet a harmadik egyenletből kivonva 0 = 1 lehet . Ezen egyenletek bármelyikének van közös megoldása. Ugyanez a jelenség tetszőleges számú egyenlet esetén előfordulhat.

Általában következetlenségek fordulnak elő, ha a rendszerben az egyenletek bal oldala lineárisan függ, és az állandó tagok nem elégítik ki a függőségi relációt. Az az egyenletrendszer, amelynek bal oldala lineárisan független, mindig konzisztens.

Másképpen fogalmazva, szerint Rouche-Capelli tétel , bármely egyenletrendszert (túlhatározott, vagy más módon) ellentmond, ha a helyezés az kiegészített mátrix nagyobb, mint a rangot a koefficiens mátrix . Ha viszont e két mátrix rangja egyenlő, akkor a rendszernek legalább egy megoldással kell rendelkeznie. A megoldás akkor és csak akkor egyedi, ha a rangsor megegyezik a változók számával. Egyébként az általános megoldás k szabad paraméterekkel rendelkezik, ahol k a változók száma és a rang közötti különbség; ezért ilyen esetekben végtelen számú megoldás létezik. Egy egyenletrendszer rangja (azaz a kibővített mátrix rangja) soha nem lehet magasabb, mint a [változók száma] + 1, ami azt jelenti, hogy a tetszőleges számú egyenletet tartalmazó rendszer mindig csökkenthető olyan rendszerre, amely rendelkezik független egyenletek száma, amely legfeljebb egyenlő a [változók számával] + 1.

Egyenértékűség

Két lineáris rendszer, amelyek ugyanazt a változóhalmazt használják, ekvivalensek, ha a második rendszer egyenletei mindegyike algebrai úton származtatható az első rendszer egyenleteiből, és fordítva. Két rendszer egyenértékű, ha mindkettő inkonzisztens, vagy mindegyik egyenlete a másik egyenleteinek lineáris kombinációja. Ebből következik, hogy két lineáris rendszer akkor és csak akkor egyenértékű, ha ugyanazzal a megoldási készlettel rendelkeznek.

Lineáris rendszer megoldása

Számos algoritmus a megoldására egy lineáris egyenletrendszer.

A megoldás leírása

Ha a megoldáshalmaz véges, akkor egyetlen elemre redukálódik. Ebben az esetben az egyedi megoldást olyan egyenletsorozat írja le, amelynek bal oldala az ismeretlenek neve, a jobb oldal pedig a megfelelő érték . Ha egy megrendelést a ismeretlenek már rögzített, például a ABC sorrendben az oldatot ki lehet leírni, mint egy vektor értékek, mint az előző példában. ${\ displaystyle (x = 3, \; y = -2, \; z = 6)}$${\ displaystyle (3, \,-2, \, 6)}$

A végtelen számú megoldást tartalmazó halmaz leírásához általában néhány változót szabadnak (vagy függetlennek vagy paraméternek ) jelölnek , ami azt jelenti, hogy bármilyen értéket felvehetnek, míg a többi változó a függvény értékeitől függ szabad változók.

Például vegye figyelembe a következő rendszert:

${\ displaystyle {\ begin {alignedat} {7} x && \;+\; && 3y && \;-\; && 2z && \; = \; && 5 & \\ 3x && \;+\; &&y 5 & & 5; ; && 7 & \ end {alignedat}}}$

Ennek a rendszernek a megoldása a következő egyenletekkel írható le:

${\ displaystyle x = -7z-1 \; \; \; \; {\ text {and}} \; \; \; \; y = 3z+2 {\ text {.}}}$

Itt z a szabad változó, míg x és y z -től függ . A megoldáshalmaz bármely pontját úgy kaphatjuk meg, hogy először kiválasztunk egy z értéket , majd kiszámítjuk az x és y megfelelő értékeket .

Minden szabad változó egy szabadságfokot ad a megoldástérnek , amelynek száma megegyezik a megoldáshalmaz méretével . Például a fenti egyenlethez tartozó megoldáshalmaz egy egyenes, mivel a megoldáshalmaz egy pontja a z paraméter értékének megadásával választható ki . Egy magasabb rendű végtelen megoldás leírhat síkot vagy magasabb dimenziójú halmazt.

A szabad változók eltérő választása ugyanannak a megoldáshalmaznak a leírását eredményezheti. Például a fenti egyenletek megoldása a következőképpen írható le:

${\ displaystyle y =-{\ frac {3} {7}} x+{\ frac {11} {7}} \; \; \; \; {\ text {és}} \; \; \; \; z =-{\ frac {1} {7}} x-{\ frac {1} {7}} {\ text {.}}}$

Itt x a szabad változó, és y és z függ.

A változók kiküszöbölése

A lineáris egyenletrendszer megoldásának legegyszerűbb módja a változók ismételt kiküszöbölése. Ez a módszer a következőképpen írható le:

1. Az első egyenletben oldja meg az egyik változót a többi tekintetében.
2. Helyettesítse ezt a kifejezést a fennmaradó egyenletekkel. Ezzel egyenletrendszert kapunk eggyel kevesebb egyenlettel és eggyel kevesebb ismeretlennel.
3. Ismételje addig, amíg a rendszer egyetlen lineáris egyenletre nem csökken.
4. Oldja meg ezt az egyenletet, majd cserélje ki, amíg meg nem találja a teljes megoldást.

Például vegye figyelembe a következő rendszert:

${\ displaystyle {\ begin {alignedat} {7} x && \;+\; && 3y && \;-\; && 2z && \; = \; && 5 & \\ 3x && \;+\; & 5y && \;+\; && 6z && \; = \ ; && 7 & \\ 2x && \;+\; && 4y && \;+\; && 3z && \; = \; && 8 & \ end {alignedat}}}$

Megoldása az első egyenlet x ad x = 5 + 2 Z - 3 y , és az ilyen típusú csatlakozás a második és a harmadik egyenlet hozamok

${\ displaystyle {\ begin {alignedat} {5} -4y && \;+\; && 12z && \ = = \; &&-8 & \\-2y && \;+\; && 7z && \ = = \; &&-2 & \ end {alignedat }}}$

Ha az első egyenletet megoldjuk y esetén, akkor y = 2 + 3 z , és ezt a második egyenletbe illesztve z = 2 lesz . Nálunk most van:

${\ displaystyle {\ begin {alignedat} {7} x && \; = \; && 5 && \;+\; && 2z && \;-\; && 3y & \\ y && \; = \; && 2 &&;+\; && 3z &&&&& \\ z && \ ; = \; && 2 &&&&&&&&& \ end {alignedat}}}$

Ha a második egyenletbe behelyettesítjük a z = 2 értéket , akkor y = 8 lesz , és ha z = 2 és y = 8 helyettesítjük az első egyenletet, akkor x = −15 lesz . Ezért a megoldáshalmaz az egyetlen pont ( x , y , z ) = (−15, 8, 2) .

Sorcsökkentés

A sorcsökkentésben (más néven Gauss -elimináció ) a lineáris rendszert kibővített mátrixként ábrázolják :

${\ displaystyle \ left [{\ begin {array} {rrr | r} 1 & 3 & -2 & 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \ end {array}} \ jobb] {\ text {.}}}$

Ezt a mátrixot azután elemi sorműveletek segítségével módosítják, amíg el nem éri a csökkentett sorú echelon formát . Háromféle elemi sorművelet létezik:

1. típus : Két sor pozíciójának felcserélése.

2. típus : Szorozzon egy sort nem nulla skalárral .

3. típus : Adja hozzá az egyik sorhoz a skalár többszörösét.

Mivel ezek a műveletek megfordíthatók, a létrehozott kibővített mátrix mindig egy lineáris rendszert képvisel, amely egyenértékű az eredetivel.

Számos speciális algoritmus létezik a kiterjesztett mátrix sorcsökkentésére, amelyek közül a legegyszerűbb a Gauss-elimináció és a Gauss-Jordan-elimináció . A következő számítás azt mutatja, hogy a Gauss – Jordan elimináció a fenti mátrixra vonatkozik:

${\ displaystyle {\ begin {aligned} \ left [{\ begin {array} {rrr | r} 1 & 3 & -2 & 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \ end {array}} \ right] & \ sim \ left [{\ begin {tömb} {rrr | r} 1 & 3 & -2 & 5 \\ 0 & -4 & 12 & -8 \\ 2 & 4 & 3 & 8 \ end {array}} \ right] \ sim \ left [{\ begin {array} {rrr | r} 1 & 3 & -2 & 5 \ \ 0 & -4 & 12 & -8 \\ 0 & -2 & 7 & -2 \ end {array}} \ right] \ sim \ left [{\ begin {array} {rrr | r} 1 & 3 & -2 & 5 \\ 0 & 1 & -3 & 2 \\ 0 &- 2 & 7 & -2 \ end {tömb}} \ jobb] \\ & \ sim \ left [{\ begin {array} {rrr | r} 1 & 3 & -2 & 5 \\ 0 & 1 & -3 & 2 \\ 0 & 0 & 1 & 2 \ end {array}} \ jobb ] \ sim \ left [{\ begin {array} {rrr | r} 1 & 3 & -2 & 5 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array}} \ right] \ sim \ left [{\ begin {array} {rrr | r } 1 & 3 & 0 & 9 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array}} \ jobb] \ sim \ bal [{\ begin {array} {rrr | r} 1 & 0 & 0 & -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array}} \ jobb ]. \ end {aligned}}}$

Az utolsó mátrix redukált soros sorban van, és az x = −15 , y = 8 , z = 2 rendszert képviseli . A változók algebrai kiküszöbölésére vonatkozó előző rész példájával való összehasonlítás azt mutatja, hogy ez a két módszer valójában ugyanaz; a különbség abban rejlik, hogy a számításokat hogyan írják le.

Cramer szabálya

Cramer szabálya a lineáris egyenletrendszer megoldásának explicit formulája, ahol minden változót két determináns hányadosa ad meg . Például a rendszer megoldása

${\ displaystyle {\ begin {alignedat} {7} x & \;+& \; 3y & \;-& \; 2z & \; = & \; 5 \\ 3x & \;+& \; 5y & \;+& \; 6z & \; = & \; 7 \\ 2x & \;+& \; 4y & \;+& \; 3z & \; = & \; 8 \ end {alignedat}}}$

által adva

${\ displaystyle x = {\ frac {\, {\ begin {vmatrix} 5 & 3 & -2 \\ 7 & 5 & 6 \\ 8 & 4 & 3 \ end {vmatrix}} \,} {\, {\ begin {vmatrix} 1 & 3 & -2 \\ 3 & 5 & 6 \\ 2 & 4 & 3 \ end {vmatrix}} \,}}, \; \; \; \; y = {\ frac {\, {\ begin {vmatrix} 1 & 5 & -2 \\ 3 & 7 & 6 \\ 2 & 8 & 3 \ end {vmatrix} } \,} {\, {\ begin {vmatrix} 1 & 3 & -2 \\ 3 & 5 & 6 \\ 2 & 4 & 3 \ end {vmatrix}} \,}}, \; \; \; \; z = {\ frac {\, { \ begin {vmatrix} 1 & 3 & 5 \\ 3 & 5 & 7 \\ 2 & 4 & 8 \ end {vmatrix}} \,} {\, {\ begin {vmatrix} 1 & 3 & -2 \\ 3 & 5 & 6 \\ 2 & 4 & 3 \ end {vmatrix}} \,}}. }$

Minden változó esetében a nevező az együtthatók mátrixának meghatározója , míg a számláló egy olyan mátrix determinánsa, amelyben az egyik oszlopot felváltotta az állandó tagú vektor.

Bár Cramer szabálya elméletileg fontos, nagy gyakorlati mátrixok esetén kevés gyakorlati értéke van, mivel a nagy determinánsok kiszámítása némileg nehézkes. (Valójában a nagy determinánsokat a legkönnyebben a sorcsökkentés segítségével lehet kiszámítani.) Továbbá a Cramer -szabály nagyon gyenge numerikus tulajdonságokkal rendelkezik, ezért alkalmatlan még kis rendszerek megbízható megoldására is, hacsak a műveleteket korlátlan pontossággal nem racionális aritmetikában hajtjuk végre.

Mátrix megoldás

Ha az egyenletrendszert mátrix formában fejezzük ki , akkor a teljes megoldáshalmaz mátrix formában is kifejezhető. Ha a mátrix A négyzetes (van m sorból és n = m oszlopok), és teljes rangú (összes m sorok független), akkor a rendszer egy egyedi megoldást által adott ${\ displaystyle A \ mathbf {x} = \ mathbf {b}}$

${\ displaystyle \ mathbf {x} = A^{-1} \ mathbf {b}}$

ahol az inverz a A . Általánosabban, függetlenül attól, hogy m = n , vagy nem, és függetlenül attól, rangot A , az összes oldat (ha vannak ilyenek) kapnak a Moore-Penrose pszeudoinverze a A , jelöljük , az alábbiak szerint: ${\ displaystyle A^{-1}}$${\ displaystyle A^{+}}$

${\ displaystyle \ mathbf {x} = A^{+} \ mathbf {b}+\ bal (IA^{+} A \ jobb) \ mathbf {w}}$

ahol van egy szabad paraméterekből álló vektor, amely minden lehetséges n × 1 vektoron átnyúlik. Minden megoldás (ok) létezéséhez szükséges és elegendő feltétel, hogy a potenciális megoldás használatával kielégítsük - vagyis azt, hogy Ha ez a feltétel nem áll fenn, akkor az egyenletrendszer inkonzisztens és nincs megoldás. Ha a feltétel fennáll, a rendszer konzisztens és legalább egy megoldás létezik. Például a fent említett esetben, amikor A négyzet alakú és teljes rangú, egyszerűen egyenlő, és az általános megoldási egyenlet egyszerűsödik ${\ displaystyle \ mathbf {w}}$${\ displaystyle \ mathbf {w} = \ mathbf {0}}$${\ displaystyle A \ mathbf {x} = \ mathbf {b}}$${\ displaystyle AA^{+} \ mathbf {b} = \ mathbf {b}.}$${\ displaystyle A^{+}}$${\ displaystyle A^{-1}}$

${\ displaystyle \ mathbf {x} = A^{-1} \ mathbf {b} +\ bal (IA^{-1} A \ jobb) \ mathbf {w} = A^{-1} \ mathbf {b } +\ bal (II \ jobb) \ mathbf {w} = A^{-1} \ mathbf {b}}$

mint korábban említettük, ahol teljesen kiesett a megoldásból, és csak egyetlen megoldás maradt. Más esetekben azonban marad, és így a szabad paramétervektor potenciális értékeinek végtelensége végtelen számú megoldást ad az egyenletnek. ${\ displaystyle \ mathbf {w}}$${\ displaystyle \ mathbf {w}}$${\ displaystyle \ mathbf {w}}$

Más módszerek

Míg a három vagy négy egyenletből álló rendszerek könnyen megoldhatók kézzel (lásd Cracovian ), a számítógépeket gyakran használják nagyobb rendszerekhez. A lineáris egyenletrendszer megoldásának standard algoritmusa bizonyos módosításokkal a Gauss -elimináción alapul. Először is el kell kerülni a kis számokkal való osztást, ami pontatlan eredményekhez vezethet. Ezt megteheti az egyenletek szükség szerinti átrendezésével, ezt a folyamatot pivoting néven ismerik . Másodszor, az algoritmus nem is pontosan minánsok, de kiszámítja az LU felbontás a mátrix egy . Ez többnyire olyan szervezeti eszköz, de sokkal gyorsabb, ha az egyik, hogy megoldja több rendszer ugyanolyan mátrix A , de különböző vektorokat b .

Ha a mátrix egy olyan különleges szerkezet, ezt ki lehet használni, így gyorsabb és pontosabb algoritmusokat. Például a szimmetrikus pozitív határozott mátrixú rendszereket kétszer gyorsabban lehet megoldani a Cholesky -bontással . A Levinson rekurzió gyors módszer Toeplitz mátrixokhoz . Különleges módszerek léteznek a sok nulla elemű mátrixokra is (úgynevezett ritka mátrixok ), amelyek gyakran megjelennek az alkalmazásokban.

A nagyon nagy rendszerek esetében gyakran teljesen más megközelítést alkalmaznak, amelyek egyébként túl sok időt vagy memóriát igényelnének. Az ötlet az, hogy a megoldás kezdeti közelítésével kell kezdeni (aminek egyáltalán nem kell pontosnak lennie), és ezt a közelítést több lépésben módosítani kell, hogy közelebb kerüljön a valódi megoldáshoz. Ha a közelítés kellően pontos, ezt tekintik a rendszer megoldásának. Ez az iteratív módszerek osztályához vezet . Néhány ritka mátrix esetében a véletlenszerűség bevezetése javítja az iteratív módszerek sebességét.

Van egy kvantum algoritmus is a lineáris egyenletrendszerekhez .

Homogén rendszerek

A lineáris egyenletrendszer homogén, ha az összes állandó tag nulla:

${\ displaystyle {\ begin {alignedat} {7} a_ {11} x_ {1} && \;+\; && a_ {12} x_ {2} && \;+\ cdots+\; && a_ {1n} x_ {n } && \; = \; &&& 0 \\ a_ {21} x_ {1} && \;+\; && a_ {22} x_ {2} && \;+\ cdots+\; && a_ {2n} x_ {n} && \; = =; mn} x_ {n} && \; = \; &&& 0. \\\ end {alignedat}}}$

A homogén rendszer egyenértékű a forma mátrixegyenletével

${\ displaystyle A \ mathbf {x} = \ mathbf {0}}$

ahol A egy m × n mátrix, x egy oszlop vektor n bejegyzéseket, és 0 a zéró vektor a m bejegyzéseket.

Homogén oldatkészlet

Minden homogén rendszernek van legalább egy megoldása, az úgynevezett nulla (vagy triviális ) megoldás, amelyet úgy kapunk, hogy mindegyik változóhoz hozzárendeljük a nulla értéket. Ha a rendszernek nincs szinguláris mátrixa ( det ( A ) ≠ 0 ), akkor ez az egyetlen megoldás. Ha a rendszernek szinguláris mátrixa van, akkor létezik egy végtelen számú megoldást tartalmazó megoldáshalmaz. Ez a megoldáskészlet a következő további tulajdonságokkal rendelkezik:

1. Ha u és v két vektor, amelyek egy homogén rendszer megoldásait képviselik, akkor az u + v vektorösszeg szintén megoldás a rendszerre.
2. Ha u egy vektor, amely egy homogén rendszer megoldását jelenti, és r bármely skalár , akkor r u is megoldás a rendszerre.

Pontosan ezek a tulajdonságok szükségesek ahhoz, hogy a megoldáshalmaz R ⁿ lineáris altere legyen . Különösen, az oldatot állítva homogén rendszer ugyanaz, mint a null helyet a megfelelő mátrix egy . A homogén rendszer numerikus megoldásai szinguláris értékbontással érhetők el .

Kapcsolat a nem homogén rendszerekkel

Szoros kapcsolat van a lineáris rendszer megoldásai és a megfelelő homogén rendszer megoldásai között:

${\ displaystyle A \ mathbf {x} = \ mathbf {b} \ qquad {\ text {és}} \ qquad A \ mathbf {x} = \ mathbf {0}.}$

Pontosabban, ha p az A x = b lineáris rendszer bármely konkrét megoldása , akkor a teljes megoldáshalmaz a következőképpen írható le:

${\ displaystyle \ left \ {\ mathbf {p} +\ mathbf {v}: \ mathbf {v} {\ text {bármilyen megoldás a}} A \ mathbf {x} = \ mathbf {0} \ right \} .}$

Geometriailag ez azt mondja, hogy a megoldás készlet A X = b egy fordítását az oldat készlet A x = 0 . Pontosabban, a sík az első képes rendszert kapunk lefordításával lineáris altér az homogén rendszerben a vektor által p .

Ez az érvelés csak akkor érvényes, ha az A x = b rendszernek van legalább egy megoldása. Ez akkor fordul elő akkor, ha a vektor b rejlik a kép a lineáris transzformáció A .

Lásd még

Megjegyzések

Hivatkozások

• Anton, Howard (1987), Elementary Linear Algebra (5. kiadás), New York: Wiley , ISBN 0-471-84819-0
• Beauregard, Raymond A .; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields , Boston: Houghton Mifflin Company , ISBN 0-395-14017-X
• Burden, Richard L .; Faires, J. Douglas (1993), Numerical Analysis (5. kiadás), Boston: Prindle, Weber és Schmidt , ISBN 0-534-93219-3
• Golub, Gene H .; Van Loan, Charles F. (1996), Matrix Computations (3. kiadás), Baltimore: Johns Hopkins University Press , ISBN 0-8018-5414-8
• Harper, Charlie (1976), Bevezetés a matematikai fizikába , New Jersey: Prentice-Hall , ISBN 0-13-487538-9

További irodalom

• Axler, Sheldon Jay (1997), Linear Algebra Done Right (2. kiadás), Springer-Verlag, ISBN 0-387-98259-0
• Lay, David C. (2005. augusztus 22.), Lineáris algebra és alkalmazásai (3. kiadás), Addison Wesley, ISBN 978-0-321-28713-7
• Meyer, Carl D. (2001. február 15.), Matrix Analysis and Applied Linear Algebra , Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8, archiválva az eredetiből 2001. március 1 -jén
• Poole, David (2006), Lineáris algebra: modern bevezetés (2. kiadás), Brooks/Cole, ISBN 0-534-99845-3
• Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9. kiadás), Wiley International
• Leon, Steven J. (2006), Lineáris algebra alkalmazásokkal (7. kiadás), Pearson Prentice Hall
• Strang, Gilbert (2005), Lineáris algebra és alkalmazásai

Külső linkek

• A Wikimedia Commons lineáris egyenletrendszeréhez kapcsolódó média