Exponenciális eloszlás - Exponential distribution

Exponenciális

Valószínűségi sűrűség függvény
Kumulatív eloszlásfüggvény
Paraméterek	${\ displaystyle \ lambda> 0,}$arány, vagy fordított skála
Támogatás	${\ displaystyle x \ in [0, \ infty)}$
PDF	${\ displaystyle \ lambda e^{-\ lambda x}}$
CDF	${\ displaystyle 1-e^{-\ lambda x}}$
Quantile	${\ displaystyle -{\ frac {\ ln (1 -p)} {\ lambda}}}$
Átlagos	${\ displaystyle {\ frac {1} {\ lambda}}}$
Középső	${\ displaystyle {\ frac {\ ln 2} {\ lambda}}}$
Mód	${\ displaystyle 0}$
Variancia	${\ displaystyle {\ frac {1} {\ lambda ^{2}}}}$
Ferdeség	${\ displaystyle 2}$
Volt. kurtosis	${\ displaystyle 6}$
Entrópia	${\ displaystyle 1- \ ln \ lambda}$
MGF	${\ displaystyle {\ frac {\ lambda} {\ lambda -t}}, {\ text {for}} t <\ lambda}$
CF	${\ displaystyle {\ frac {\ lambda} {\ lambda -it}}}$
Fisher információ	${\ displaystyle {\ frac {1} {\ lambda ^{2}}}}$
Kullback-Leibler divergencia	${\ displaystyle \ ln {\ frac {\ lambda _ {0}} {\ lambda}}+{\ frac {\ lambda} {\ lambda _ {0}}}-1}$

A valószínűségszámítás és a statisztika , az exponenciális eloszlás a valószínűségi eloszlása az idő közötti eseményeket Poisson folyamat , azaz egy olyan folyamat, amelyben az események fordulnak elő folyamatosan, függetlenül állandó átlagosan. Ez a gammaeloszlás sajátos esete . Ez a geometriai eloszlás folyamatos analógja , és a legfontosabb tulajdonsága, hogy memória nélküli . Amellett, hogy a Poisson -pont folyamatok elemzésére használják, számos más összefüggésben is megtalálható.

Az exponenciális eloszlás nem ugyanaz, mint az osztály exponenciális családok disztribúció, amely egy nagy osztálya valószínűségi eloszlás, amely magában foglalja az exponenciális eloszlás egyik tagja, hanem magában foglalja a normális eloszlás , binomiális eloszlás , gamma-eloszlás , Poisson , és sokan mások.

Definíciók

Valószínűségi sűrűség függvény

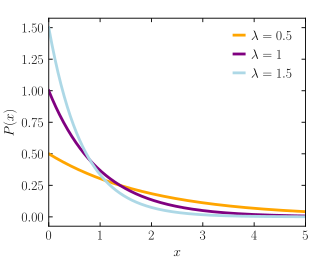
Az exponenciális eloszlás valószínűségi sűrűségfüggvénye (pdf) az

${\ displaystyle f (x; \ lambda) = {\ begin {case} \ lambda e^{-\ lambda x} & x \ geq 0, \\ 0 & x <0. \ end {tok}}}$

Itt λ > 0 az eloszlás paramétere, amelyet gyakran sebességparaméternek neveznek . Az eloszlást a [0, ∞) intervallum támogatja  . Ha egy X véletlen változó ilyen eloszlású, akkor X ~ Exp ( λ ) -t írunk  .

Az exponenciális eloszlás végtelen oszthatóságot mutat .

Kumulatív eloszlásfüggvény

A kumulatív eloszlásfüggvényt a

${\ displaystyle F (x; \ lambda) = {\ begin {case} 1-e^{-\ lambda x} & x \ geq 0, \\ 0 & x <0. \ end {tok}}}$

Alternatív paraméterezés

Az exponenciális eloszlást néha a β = 1/ λ skálaparaméter szerint parametrizálják , ami egyben az átlag is:

Tulajdonságok

Átlag, szórás, pillanatok és medián

Az X exponenciálisan eloszló véletlen változó átlagát vagy várható értékét a λ sebességparaméterrel adja meg

Az alábbi példák fényében ez logikus: ha óránként átlagosan 2 hívást kap, akkor fél órát várhat minden hívásra.

A variancia a X adják

tehát a szórás megegyezik az átlaggal.

A pillanatok az X , az Ön által megadott ${\ displaystyle n \ in \ mathbb {N}}$

A központi pillanatok az X , az Ön által megadott ${\ displaystyle n \ in \ mathbb {N}}$

ahol ! n jelentése a subfactorial az N

A medián az X adják

ahol ln a természetes logaritmusra utal . Így az átlag és a medián közötti abszolút különbség

a közép-egyenlőtlenségnek megfelelően .

Emléktelenség

Egy exponenciálisan eloszló T véletlen változó engedelmeskedik a relációnak

Ez látható a kiegészítő kumulatív eloszlásfüggvény figyelembevételével :

Ha T úgy értelmezik, mint egy esemény várakozási idejét egy kezdeti időhöz képest, akkor ez az összefüggés azt jelenti, hogy ha T feltételezi, hogy az eseményt bizonyos kezdeti s időtartam alatt nem figyelik meg , akkor a fennmaradó várakozási idő eloszlása megegyezik az eredeti feltétel nélküli elosztással. Például, ha egy esemény nem következett be 30 másodperc után, a feltételes valószínűsége, hogy az esemény legalább 10 másodpercig tart, megegyezik azzal a feltétel nélküli valószínűséggel, hogy az esemény több mint 10 másodperccel a kezdeti időpont után figyelhető meg.

Az exponenciális eloszlás és a geometriai eloszlás is csak valószínűségi eloszlás örökifjú .

Következésképpen az exponenciális eloszlás szükségszerűen az egyetlen folyamatos valószínűségi eloszlás is, amelynek állandó meghibásodási aránya van .

Quantiles

A kvantilis függvény (fordított kumulatív eloszlásfüggvény) Exp ( λ ) esetén

A kvartilisek tehát:

• első kvartilis: ln (4/3)/ λ
• medián : ln (2)/ λ
• harmadik kvartilis: ln (4)/ λ

Ennek következtében az interkvartilis tartomány ln (3)/ λ .

Kullback – Leibler divergencia

A irányított Kullback-Leibler divergencia a NAT a ( „közelítő” elosztás) ( „valódi” eloszlás) adják ${\ displaystyle e^{\ lambda}}$${\ displaystyle e^{\ lambda _ {0}}}$

Maximális entrópiaeloszlás

A [0, ∞) alátámasztással és μ átlaggal rendelkező minden valószínűségi eloszlás közül a legnagyobb λ = 1/ μ exponenciális eloszlás a legnagyobb differenciális entrópia . Más szavakkal, ez az X véletlen változó legnagyobb entrópiás valószínűségi eloszlása , amely nagyobb vagy egyenlő nullával, és amelyre E [ X ] rögzített.

Az exponenciális véletlen változók minimumának eloszlása

Let X ₁ , ..., X _n lehet független exponenciális eloszlású valószínűségi változók paraméterek alapján λ ₁ , ..., λ _n . Azután

szintén exponenciálisan oszlik el, paraméterrel

Ez látható a kiegészítő kumulatív eloszlásfüggvény figyelembevételével :

A minimumot elérő változó indexe a kategorikus eloszlás szerint oszlik meg

Egy bizonyíték látható a bérbeadással . Azután, ${\ displaystyle I = \ operatornév {argmin} _ {i \ in \ {1, \ dotsb, n \}} \ {X_ {1}, \ dotsc, X_ {n} \}}$

Vegye figyelembe, hogy

nincs exponenciálisan elosztva.

Az iid exponenciális sorrend statisztikájának közös pillanatai

Hagy legyen független, egyforma eloszlású exponenciális valószínűségi változók paraméterrel λ . Hagyja jelölik a megfelelő sorrendben statisztika . Mert , a közös pillanatban a rendelési statisztikák és megadja ${\ displaystyle X_ {1}, \ dotsc, X_ {n}}$${\ displaystyle n}$ ${\ displaystyle X _ {(1)}, \ dotsc, X _ {(n)}}$${\ displaystyle i <j}$${\ displaystyle \ operatornév {E} \ left [X _ {(i)} X _ {(j)} \ right]}$${\ displaystyle X _ {(i)}}$${\ displaystyle X _ {(j)}}$

Ez látható a teljes elvárás törvényére és az emlékezet nélküli tulajdonra hivatkozva:

Az első egyenlet a teljes elvárás törvényéből következik . A második egyenlet azt a tényt használja ki, hogy ha feltételhez kötöttük , akkor ezt követnie kell . A harmadik egyenlet támaszkodik örökifjú tulajdonság helyére a . ${\ displaystyle X _ {(i)} = x}$${\ displaystyle X _ {(j)} \ geq x}$${\ displaystyle \ operatornév {E} \ left [X _ {(j)} \ mid X _ {(j)} \ geq x \ right]}$${\ displaystyle \ operatornév {E} \ left [X _ {(j)} \ right]+x}$

Két független exponenciális véletlen változó összege

A két független véletlen változó összegének valószínűségi eloszlási függvénye (PDF) az egyes PDF -ek konvolúciója . Ha és független exponenciális valószínűségi változók megfelelő paraméterek alapján , és akkor annak a valószínűsége sűrűsége adja ${\ displaystyle X_ {1}}$${\ displaystyle X_ {2}}$${\ displaystyle \ lambda _ {1}}$${\ displaystyle \ lambda _ {2},}$${\ displaystyle Z = X_ {1}+X_ {2}}$

Ennek az eloszlásnak az entrópiája zárt formában áll rendelkezésre: feltételezve (az általánosság elvesztése nélkül), akkor ${\ displaystyle \ lambda _ {1}> \ lambda _ {2}}$ ahol az Euler-Mascheroni állandó , és a digamma függvény . ${\ displaystyle \ gamma}$${\ displaystyle \ psi (\ cdot)}$

Egyenértékű paraméterek esetén az eredmény 2 -es alakú

Erlang -eloszlás és paraméter, amely viszont a gammaeloszlás speciális esete . ${\ displaystyle \ lambda,}$

Kapcsolódó disztribúciók

• Ha akkor |

X - μ | ~ Exp (β).${\ displaystyle X \ sim \ operatornév {Laplace} \ left (\ mu, \ beta ^{-1} \ right)}$

Ha X ~ Pareto (1, λ), akkor log ( X ) ~ Exp (λ).

Ha X ~ SkewLogistic (θ), akkor .${\ displaystyle \ log \ left (1+e^{-X} \ right) \ sim \ operatorname {Exp} (\ theta)}$

Ha X _i ~ U (0, 1) akkor

$${\ displaystyle \ lim _ {n \ to \ infty} n \ min \ left (X_ {1}, \ ldots, X_ {n} \ right) \ sim \ operatorname {Exp} (1)}$$

Az exponenciális eloszlás a skálázott bétaeloszlás határa :

$${\ displaystyle \ lim _ {n \ to \ infty} n \ operatornév {Béta} (1, n) = \ operatornév {Exp} (1).}$$

Az exponenciális eloszlás a 3. típusú Pearson -eloszlás speciális esete .

Ha X ~ Exp (λ) és X _i ~ Exp (λ _i ), akkor:

• ${\ displaystyle kX \ sim \ operatornév {Exp} \ left ({\ frac {\ lambda} {k}} \ right)}$, lezárás skálázás mellett pozitív tényezővel.
• 1 +  X ~ BenktanderWeibull (λ, 1), amely csonka exponenciális eloszlásra

redukál .

ke ^X ~ Pareto ( k , λ).

e ^−X ~ Béta (λ, 1).

1/ke ^X ~ PowerLaw ( k , λ)

${\ displaystyle {\ sqrt {X}} \ sim \ operatornév {Rayleigh} \ bal ({\ frac {1} {\ sqrt {2 \ lambda}}} \ jobb)}$, a Rayleigh -eloszlás

${\ displaystyle X \ sim \ operatornév {Weibull} \ bal ({\ frac {1} {\ lambda}}, 1 \ jobb)}$, a Weibull disztribúció

${\ displaystyle X ^{2} \ sim \ operatorname {Weibull} \ left ({\ frac {1} {\ lambda ^{2}}}, {\ frac {1} {2}} \ right)}$

μ - β log (λ X ) ∼ Gumbel (μ, β) .

${\ displaystyle \ lfloor X \ rfloor \ sim \ operatornév {Geometric} \ left (1-e^{-\ lambda} \ right)}$, geometriai eloszlás a 0,1,2,3, ...

${\ displaystyle \ lceil X \ rceil \ sim \ operatornév {Geometric} \ left (1-e^{-\ lambda} \ right)}$, geometriai eloszlás az 1,2,3,4, ...

Ha szintén Y ~ Erlang ( n , λ), vagy akkor${\ displaystyle Y \ sim \ Gamma \ left (n, {\ frac {1} {\ lambda}} \ right)}$${\ displaystyle {\ frac {X} {Y}}+1 \ sim \ operatornév {Pareto} (1, n)}$

Ha továbbá λ ~ Gamma ( k , θ) (alak, skála parametrizációját), akkor a marginális eloszlása X jelentése Lomax ( k , 1 / θ), a gamma- keverék

λ ₁ X ₁ - λ ₂ Y ₂ ~ Laplace (0, 1) .

min { X ₁ , ..., X _n } ~ Exp (λ ₁ + ... + λ _n ).

Ha szintén λ _i = λ, akkor:

• ${\ displaystyle X_ {1} +\ cdots +X_ {k} = \ sum _ {i} X_ {i} \ sim}$ Erlang ( k , λ) = Gamma ( k , λ ⁻¹ ) = Gamma ( k , λ) (a ( k , θ) és (α, β) paraméterezésben) k egész alakú paraméterrel.
• X _i - X _j ~ Laplace (0, λ ⁻¹ ).

Ha továbbá XA _i függetlenek, akkor:

• ${\ displaystyle {\ frac {X_ {i}} {X_ {i}+X_ {j}}}}$~ U (0, 1)
• ${\ displaystyle Z = {\ frac {\ lambda _ {i} X_ {i}} {\ lambda _ {j} X_ {j}}}}$valószínűségi sűrűség funkcióval rendelkezik . Ezt fel lehet használni, így a

megbízhatósági intervallum számára .${\ displaystyle f_ {Z} (z) = {\ frac {1} {(z+1)^{2}}}}$${\ displaystyle {\ frac {\ lambda _ {i}} {\ lambda _ {j}}}}$

Ha szintén λ = 1:

• ${\ displaystyle \ mu-\ beta \ log \ left ({\ frac {e^{-X}} {1-e^{-X}}} \ right) \ sim \ operatorname {Logistic} (\ mu, \ béta)}$, a logisztikai eloszlás
• ${\ displaystyle \ mu -\ beta \ log \ left ({\ frac {X_ {i}} {X_ {j}}} \ right) \ sim \ operatorname {Logistic} (\ mu, \ beta)}$
• μ - σ log ( X ) ~ GEV (μ, σ, 0) .
• Ha tovább, akkor (

K-eloszlás )${\ displaystyle Y \ sim \ Gamma \ left (\ alpha, {\ frac {\ beta} {\ alpha}} \ right)}$${\ displaystyle {\ sqrt {XY}} \ sim \ operatornév {K} (\ alfa, \ béta)}$

Ha szintén λ = 1/2, akkor X ∼ χ²
₂; azaz X egy chi-négyzet eloszlás 2 szabadsági fokkal . Ennélfogva:

$${\ displaystyle \ operatornév {Exp} (\ lambda) = {\ frac {1} {2 \ lambda}} \ operatornév {Exp} \ bal ({\ frac {1} {2}} \ jobb) \ sim {\ frac {1} {2 \ lambda}} \ chi _ {2}^{2} \ Jobbra mutató nyíl \ sum _ {i = 1}^{n} \ operatornév {Exp} (\ lambda) \ sim {\ frac {1 } {2 \ lambda}} \ chi _ {2n}^{2}}$$

Ha és ~

Poisson ( X ), akkor ( geometriai eloszlás )${\ displaystyle X \ sim \ operatornév {Exp} \ left ({\ frac {1} {\ lambda}} \ right)}$${\ displaystyle Y \ X közepén}$${\ displaystyle Y \ sim \ operatornév {Geometric} \ left ({\ frac {1} {1+ \ lambda}} \ right)}$

A Hoyt -eloszlás exponenciális eloszlásból és

arcsine -eloszlásból nyerhető

Egyéb kapcsolódó disztribúciók:

• Hiper-exponenciális eloszlás- az az eloszlás, amelynek sűrűsége az exponenciális sűrűségek súlyozott összege.
• Hypoexponenciális eloszlás - az exponenciális véletlen változók általános összegének eloszlása.
• exGauss -eloszlás - az exponenciális eloszlás és a normális eloszlás összege .

Statisztikai következtetés

Az alábbiakban, tegyük fel, valószínűségi változó X exponenciális eloszlású paraméterrel λ, és amelyek

n független mintát a X , minta átlag . ${\ displaystyle x_ {1}, \ dotsc, x_ {n}}$${\ displaystyle {\ bar {x}}}$

Paraméterbecslés

A λ maximális valószínűségi becslője a következőképpen épül fel:

A λ valószínűségi függvénye a független és azonos eloszlású x = ( x ₁ ,…, x _n ) minta alapján, amely a változóból származik:

$${\ displaystyle L (\ lambda) = \ prod _ {i = 1} ^{n} \ lambda \ exp (-\ lambda x_ {i}) = \ lambda ^{n} \ exp \ left (-\ lambda \ összeg _ {i = 1} ^{n} x_ {i} \ jobb) = \ lambda ^{n} \ exp \ bal (-\ lambda n {\ overline {x}} \ jobb),}$$

ahol:

$${\ displaystyle {\ overline {x}} = {\ frac {1} {n}} \ sum _ {i = 1}^{n} x_ {i}}$$

a minta átlaga.

A valószínűségi függvény logaritmusának deriváltja:

$${\ displaystyle {\ frac {d} {d \ lambda}} \ ln L (\ lambda) = {\ frac {d} {d \ lambda}} \ left (n \ ln \ lambda -\ lambda n {\ overline {x}} \ right) = {\ frac {n} {\ lambda}}-n {\ overline {x}} \ {\ begin {case}> 0, és 0 <\ lambda <{\ frac {1} { \ overline {x}}}, \\ [8pt] = 0, & \ lambda = {\ frac {1} {\ overline {x}}}, \\ [8pt] <0, & \ lambda> {\ frac {1} {\ overline {x}}}. \ End {case}}}$$

Következésképpen a sebességparaméter maximális valószínűségi becslése a következő:

$${\ displaystyle {\ widehat {\ lambda}} _ {\ text {mle}} = {\ frac {1} {\ overline {x}}} = {\ frac {n} {\ sum _ {i} x_ { én}}}}$$

Ez nem egy torzítatlan becslése a bár

a torzítatlan becslése MLE és az elosztási átlag. ${\ displaystyle \ lambda,}$${\ displaystyle {\ overline {x}}}$ ${\ displaystyle 1/\ lambda}$

A torzítás egyenlő ${\ displaystyle {\ widehat {\ lambda}} _ {\ text {mle}}}$

$${\ displaystyle b \ equiv \ operatornév {E} \ left [\ left ({\ widehat {\ lambda}} _ {\ text {mle}}-\ lambda \ right) \ right] = {\ frac {\ lambda} {n-1}}}$$

amely az elfogultsággal korrigált maximális valószínűségi becslőt adja

$${\ displaystyle {\ widehat {\ lambda}} _ {\ text {mle}}^{*} = {\ widehat {\ lambda}} _ {\ text {mle}}-{\ widehat {b}}.}$$

A várható négyzetes hiba hozzávetőleges minimalizálója

Tegyük fel, hogy legalább három mintája van. Ha a várható átlagos négyzethiba minimalizálóját (lásd még: Előrehajlás – variancia kompromisszum ) keressük , amely hasonló a maximális valószínűségi becsléshez (azaz a valószínűségi becslés multiplikatív korrekciója):

$${\ displaystyle {\ widehat {\ lambda}} = \ bal ({\ frac {n-2} {n}} \ jobb) \ bal ({\ frac {1} {\ bar {x}}} \ jobb) = {\ frac {n-2} {\ összeg _ {i} x_ {i}}}}$$

Ez származik az átlag és szórás az inverz gamma-eloszlás : . ${\ texttyle {\ mbox {Inv-Gamma}} (n, \ lambda)}$

Fisher információ

A Fisher-információ , jelöljük , egy becslés az arány paraméter adják: ${\ displaystyle {\ mathcal {I}} (\ lambda)}$${\ displaystyle \ lambda}$

$${\ displaystyle {\ mathcal {I}} (\ lambda) = \ operatornév {E} \ bal [\ bal. \ bal lambda) \ jobb)^{2} \ jobb | \ lambda \ jobb] = \ int \ bal ({\ frac {\ részleges {\ részleges \ lambda}} \ log f (x; \ lambda) \ jobb)^ {2} f (x; \ lambda) \, dx}$$

Az elosztás és a megoldás csatlakoztatása a következőket eredményezi:

$${\ displaystyle {\ mathcal {I}} (\ lambda) = \ int _ {0}^{\ infty} \ left ({\ frac {\ partial} {\ daļ \ lambda}} \ log \ lambda e^{ -\ lambda x} \ jobb)^{2} \ lambda e^{-\ lambda x} \, dx = \ int _ {0}^{\ infty} \ bal ({\ frac {1} {\ lambda} } -x \ jobb)^{2} \ lambda e^{-\ lambda x} \, dx = \ lambda^{-2}.}$$

Ez határozza meg, hogy az exponenciális eloszlás minden független mintája milyen mennyiségű információt hordoz az ismeretlen sebességparaméterről . ${\ displaystyle \ lambda}$

Bizalmi intervallumok

Az exponenciális eloszlás sebességparaméterének 100 (1 - α)% -os konfidencia intervallumát a következők adják meg:

$${\ displaystyle {\ frac {2n} {{\ widehat {\ lambda}} \ chi _ {1-{\ frac {\ alpha} {2}}, 2n}^{2}}} <{\ frac {1 } {\ lambda}} <{\ frac {2n} {{\ widehat {\ lambda}} \ chi _ {{\ frac {\ alpha} {2}}, 2n}^{2}}}}$$

ami szintén egyenlő:

$${\ displaystyle {\ frac {2n {\ overline {x}}} {\ chi _ {1-{\ frac {\ alpha} {2}}, 2n}^{2}}} <{\ frac {1} {\ lambda}} <{\ frac {2n {\ overline {x}}} {\ chi _ {{\ frac {\ alpha} {2}}, 2n}^{2}}}}$$

ahol χ²
_{p , v}a 100 ( p ) percentilis a Chi-négyzet-eloszlás a v szabadsági fokkal , n a megfigyelések száma közötti érkezési idők a mintában, és az X-bár a minta átlagos. Egy egyszerű közelítés a pontos intervallum végpontok származtatható a normál közelítés a χ²
_{p , v}terjesztés. Ez a közelítés 95% -os megbízhatósági intervallumra a következő értékeket adja:

$${\ displaystyle {\ begin {aligned} \ lambda _ {\ text {alsó}} & = {\ widehat {\ lambda}} \ bal (1-{\ frac {1.96} {\ sqrt {n}}} \ jobb ) \\\ lambda _ {\ text {felső}} & = {\ widehat {\ lambda}} \ bal (1+{\ frac {1.96} {\ sqrt {n}}} \ jobb) \ end {aligned} }}$$

Ez a közelítés elfogadható legalább 15-20 elemet tartalmazó minták esetén.

Bayesi következtetés

Az exponenciális eloszlás előtti konjugátum a gamma -eloszlás (amelynek különleges esete az exponenciális eloszlás). A gamma valószínűségi sűrűség függvény alábbi paraméterezése hasznos:

$${\ displaystyle \ operatornév {Gamma} (\ lambda; \ alfa, \ beta) = {\ frac {\ beta ^{\ alpha}} {\ Gamma (\ alfa)}} \ lambda ^{\ alfa -1} \ exp (-\ lambda \ béta).}$$

A

p posterior eloszlást ezután a fent meghatározott valószínűségi függvény és egy gamma előtti kifejezéssel lehet kifejezni:

Most a p hátsó sűrűséget megadtuk egy hiányzó normalizáló állandóig. Mivel gamma pdf formátumú, ez könnyen kitölthető, és a következőket kapja:

Itt az α hiperparaméter az előző megfigyelések számaként értelmezhető, a β pedig a korábbi megfigyelések összegeként. A hátsó átlag itt a következő:

Előfordulás és alkalmazások

Az események előfordulása

Az exponenciális eloszlás természetesen akkor következik be, amikor egy homogén Poisson-folyamatban leírjuk az érkezési idők hosszát .

Az exponenciális eloszlás a geometriai eloszlás folyamatos párjának tekinthető , amely leírja a Bernoulli -kísérletek számát, amelyek szükségesek a diszkrét folyamat állapotának megváltoztatásához. Ezzel szemben az exponenciális eloszlás leírja a folyamatos folyamat állapotváltozásának idejét.

A valós forgatókönyvekben az állandó arány (vagy időegységre eső valószínűség) feltételezése ritkán teljesül. Például a bejövő telefonhívások aránya a napszaktól függően eltérő. De ha egy olyan időintervallumra összpontosítunk, amely alatt az arány nagyjából állandó, például 14 és 16 óra között a munkanapokon, akkor az exponenciális eloszlás jó közelítő modellként használható a következő telefonhívás beérkezéséig. Hasonló figyelmeztetések vonatkoznak a következő példákra, amelyek megközelítőleg exponenciálisan eloszló változókat eredményeznek:

• A radioaktív részecske lebomlásáig eltelt idő , vagy a Geiger -számláló kattintásai közötti idő
• A következő telefonhívásig eltelt idő
• A nemteljesítésig eltelt idő (a vállalati adósság tulajdonosainak történő kifizetéskor) csökkentett hitelkockázati modellezésben

Az exponenciális változók felhasználhatók olyan helyzetek modellezésére is, amikor bizonyos események egységnyi hosszúságonként állandó valószínűséggel fordulnak elő, például a DNS -szál mutációi közötti távolság vagy az adott útszakaszok közötti távolság .

A sorbanállás elméletében a rendszerben az ügynökök kiszolgálási idejét (pl. Mennyi időbe telik, amíg a bankpénztár stb. Kiszolgálja az ügyfelet) gyakran exponenciálisan elosztott változóként modellezik. (Például az ügyfelek érkezését a Poisson -eloszlás is modellezi, ha az érkezők függetlenek és azonos módon vannak elosztva.) A folyamat hossza, amely több független feladat sorozatának tekinthető, követi az Erlang -eloszlást (ami az eloszlás több független exponenciálisan eloszló változó összegéből). A megbízhatóságelmélet és a megbízhatósági tervezés is széles körben használja az exponenciális eloszlást. Mivel a memória nélküli tulajdonsága ez az eloszlás, ez jól alkalmas arra, hogy modellezzük a konstans kockázati arány része fürdőkádgörbe használt a megbízhatóság elméletben. Ez azért is nagyon kényelmes, mert olyan könnyű hozzáadni a hibaarányokat egy megbízhatósági modellben. Az exponenciális eloszlás azonban nem megfelelő az élőlények vagy a technikai eszközök teljes élettartamának modellezésére, mert a "meghibásodási arányok" itt nem állandóak: több hiba fordul elő nagyon fiatal és nagyon öreg rendszerek esetében.

A fizikában , ha egy gázt rögzített hőmérsékleten és nyomáson figyel meg egységes gravitációs mezőben , a különböző molekulák magassága is közelítő exponenciális eloszlást követ, amelyet barometrikus képletnek neveznek . Ez az alábbiakban említett entrópia tulajdonság következménye.

A hidrológiában az exponenciális eloszlást használják olyan változók szélső értékeinek elemzésére, mint a havi és éves maximális napi csapadék és a folyók vízhozamának értékei.

A kék kép egy példát illusztrál arra, hogy az exponenciális eloszlást illesztettük az éves maximum egynapos csapadékhoz, és a binomiális eloszlás alapján a 90% -os megbízhatósági öv is megjelenik . A csapadékadatokat az összesített gyakorisági elemzés részeként ábrázolják .

A műtők menedzsmentjében a műtét időtartamának megoszlása ​​a műtétek egy kategóriájában, ahol nincs tipikus munkahálózat (például a sürgősségi osztályon , amely minden típusú műtétet magában foglal).

Jóslás

Miután ismeretlen exponenciális eloszlásból n adatpontból álló mintát figyeltünk meg, gyakori feladat, hogy ezeket a mintákat használva előrejelzéseket készítünk az ugyanabból a forrásból származó jövőbeli adatokról. Gyakori prediktív eloszlás a jövőbeli minták között az úgynevezett plug-in eloszlás, amelyet úgy alakítanak ki, hogy az λ sebességparaméter megfelelő becslését az exponenciális sűrűség függvénybe kapcsolják . A becslés gyakori választása a maximális valószínűség elve által biztosított, és ennek használatával a megjósolt sűrűség jön létre egy jövőbeli x _{n +1} mintán , a megfigyelt x = ( x ₁ , ..., x _n ) mintákon által adott

A Bayes -féle megközelítés olyan prediktív eloszlást biztosít, amely figyelembe veszi a becsült paraméter bizonytalanságát, bár ez döntően függhet a prior kiválasztásától.

A prediktív eloszlás mentes a szubjektív bayesi megközelítés alapján felmerülő prioritások kiválasztásának kérdéseitől

amelyet úgy tekinthetünk

1. gyakori bizalmi eloszlás , amelyet a kulcsfontosságú mennyiség eloszlásából kapunk ;${\ displaystyle {x_ {n+1}}/{\ overline {x}}}$
2. egy profil -prediktív valószínűség, amelyet úgy kapunk, hogy a λ paramétert maximalizálással kizárjuk az x _{n +1} és λ együttes valószínűségből ;
3. objektív bayesi prediktív posterior eloszlás, amelyet a nem informatív Jeffreys 1/ λ felhasználásával kaptak ;
4. a feltételes normalizált maximális valószínűség (CNML) prediktív eloszlását, információelméleti megfontolásokból.

A prediktív eloszlás pontossága mérhető a valódi exponenciális eloszlás ( λ ₀₎ paraméter és az x mintán alapuló prediktív eloszlás közötti távolság vagy eltérés használatával . A Kullback – Leibler divergencia a két eloszlás közötti különbség általánosan használt, paraméterezés nélküli mértéke. Ha Δ ( λ ₀ || p ) a Kullback – Leibler eltérést jelöli a λ ₀ sebességparaméteres exponenciális érték és a p prediktív eloszlás között , akkor kimutatható, hogy

ahol a várakozást az λ ₀ ∈ (0, ∞) sebességparaméterű exponenciális eloszlás tekintetében vesszük , és ψ (·) a digamma függvény. Világos, hogy a CNML prediktív eloszlása ​​minden n > 0 mintaméret tekintetében az átlagos Kullback – Leibler divergencia tekintetében szigorúan meghaladja a maximális valószínűségi plug-in eloszlást .

Számítási módszerek

Exponenciális variánsok generálása

Az exponenciális változók előállítására szolgáló, koncepcionálisan nagyon egyszerű módszer az inverz transzformációs mintavételezésen alapul : Adott egy véletlenszerű U változó, amelyet az egységintervallum (0, 1) egyenletes eloszlásából vontak le , a változó

exponenciális eloszlással rendelkezik, ahol F ⁻¹ a kvantilis függvény , amelyet a

Ezenkívül, ha U egyenletes a (0, 1), akkor az 1 - U is . Ez azt jelenti, hogy exponenciális variánsokat lehet előállítani az alábbiak szerint:

Az exponenciális variánsok előállításának más módszereit Knuth és Devroye tárgyalja.

Rendelkezésre áll egy gyors módszer arra is, hogy készen álló exponenciális változatokat készítsünk rendezési rutin használata nélkül.

Lásd még

• Holtidő - az exponenciális eloszlás alkalmazása a részecskék detektor elemzésére.
• Laplace -eloszlás , vagy a "kettős exponenciális eloszlás".
• Valószínűségi eloszlások összefüggései
• Marshall – Olkin exponenciális eloszlás

Hivatkozások

Külső linkek

• "Exponenciális eloszlás" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Exponenciális eloszlás online kalkulátora