Inverz hiperbolikus függvények - Inverse hyperbolic functions

A matematika , a inverz hiperbolikus függvények a inverz függvények a hiperbolikus függvények .

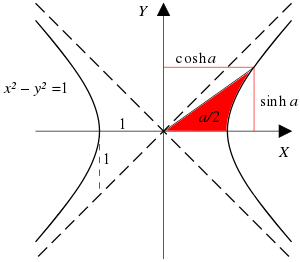
A hiperbolikus függvény adott értékéhez a megfelelő inverz hiperbolikus függvény biztosítja a megfelelő hiperbolikus szöget . A méret a hiperbolikus szög egyenlő a területen a megfelelő hiperbolikus szektor a hiperbola xy = 1 , vagy területének kétszerese a megfelelő szektor a készülék hiperbola x ² - y ² = 1 , csak mint egy kör alakú szög kétszerese a terület a körcikk az egység kör . Egyes szerzők az inverz hiperbolikus függvényeket " területfüggvényeknek " nevezték a hiperbolikus szögek megvalósításához.

A hiperbolikus függvények a szögek és távolságok számításában fordulnak elő a hiperbolikus geometriában . Azt is előfordul a megoldások számos lineáris differenciálegyenletek (mint például az egyenlet meghatározó felsővezeték ), köbös egyenletek , és a Laplace-egyenlet a derékszögű koordináta . Laplace egyenletei fontosak a fizika számos területén , beleértve az elektromágneses elméletet , a hőátadást , a folyadékdinamikát és a speciális relativitáselméletet .

Jelölés

A leggyakoribb rövidítések az ISO 80000-2 szabvány előírásai. Ezek közé tartozik a ar- rövidítése követ a megfelelő hiperbolikus funkciót (pl, arsinh, arcosh).

Azonban, ARC , majd a megfelelő hiperbolikus funkciót (pl, arcsinh, arccosh) is gyakran látható, hasonlóan a nómenklatúrát inverz trigonometrikus függvények . Ezek téves jelzők, mivel az ív előtag az arcus rövidítése , míg az ar előtag a területet jelenti ; a hiperbolikus függvények nem kapcsolódnak közvetlenül az ívekhez.

Más szerzők inkább az arg sinh, argcosh, argtanh és így tovább jelöléseket használják , ahol az arg előtag a latin argumentum rövidítése . A számítástechnikában ezt gyakran lerövidítik ash -ra .

A sinh ⁻¹ ( x ) , cosh ⁻¹ ( x ) stb. Jelölést is használják, annak ellenére, hogy vigyázni kell arra, hogy elkerüljük a -1 − felső index hatalmi értelmezését, szemben a rövidítéssel. az inverz függvény (pl. cosh ⁻¹ ( x ) versus cosh ( x ) ⁻¹ ).

Definíciók a logaritmusok szempontjából

Mivel a hiperbolikus függvények vannak racionális függvények a e ^x amelynek számláló és a nevező is a foka legfeljebb két, ezeket a funkciókat meg lehet oldani szempontjából e ^x , segítségével a másodfokú képlet ; akkor a természetes logaritmus felvételével a következő kifejezéseket kapjuk az inverz hiperbolikus függvényekhez.

Mert bonyolult érveket, az inverz hiperbolikus függvények, a négyzetgyök és a logaritmus is több értékes funkciók , és az egyenletek a következő alfejezetben lehet tekinteni egyenletek multi-értékű függvények.

Minden inverz hiperbolikus függvény esetében (kivéve az inverz hiperbolikus kotangent és az inverz hiperbolikus kozekánsokat) a valós függvény tartománya kapcsolódik .

Fordított hiperbolikus szinusz

Inverz hiperbolikus szinusz (más néven terület hiperbolikus szinusz) (latinul: Area sinus hyperbolicus ):

${\ displaystyle \ operatornév {arsinh} x = \ ln \ left (x+{\ sqrt {x^{2} +1}} \ right)}$

A tartomány az egész valódi vonal .

Fordított hiperbolikus koszinusz

Inverz hiperbolikus koszinusz (más néven terület hiperbolikus koszinusz ) (latinul: Area cosinus hyperbolicus ):

${\ displaystyle \ operatornév {arcosh} x = \ ln \ left (x+{\ sqrt {x^{2} -1}} \ right)}$

A tartomány a zárt intervallum [1, +∞) .

Fordított hiperbolikus érintő

Inverz hiperbolikus érintő (más néven a rea hiperbolikus érintő ) (latinul: Area tangens hyperbolicus ):

${\ displaystyle \ operatornév {artanh} x = {\ frac {1} {2}} \ ln \ left ({\ frac {1+x} {1-x}} \ right)}$

A tartomány a nyitott intervallum (−1, 1) .

Fordított hiperbolikus kotangens

Inverz hiperbolikus kotangens (más néven terület hiperbolikus kotangens ) (latinul: Area cotangens hyperbolicus ):

${\ displaystyle \ operatornév {arcoth} x = {\ frac {1} {2}} \ ln \ left ({\ frac {x+1} {x-1}} \ right)}$

A tartomány a nyitott intervallumok (−∞, −1) és (1, +∞) egyesítése .

Fordított hiperbolikus szekáns

Inverz hiperbolikus secant (más néven terület hiperbolikus secant ) (latinul: Area secans hyperbolicus ):

${\ displaystyle \ operatornév {arsech} x = \ ln \ left ({\ frac {1} {x}}+{\ sqrt {{\ frac {1} {x^{2}}}-1}} \ jobb ) = \ ln \ bal ({\ frac {1+{\ sqrt {1-x^{2}}}} {x}} \ jobb)}$

A tartomány a félig nyitott intervallum (0, 1) .

Fordított hiperbolikus kozekáns

Inverz hiperbolikus kozekáns (más néven terület hiperbolikus kozekáns ) (latinul: Area cosecans hyperbolicus ):

${\ displaystyle \ operatornév {arcsch} x = \ ln \ left ({\ frac {1} {x}}+{\ sqrt {{\ frac {1} {x^{2}}}+1}} \ jobb )}$

A tartomány az igazi vonal, 0 eltávolítva.

Összeadási képletek

${\ displaystyle \ operatnev ^{2}}} \ ugye)}$

${\ displaystyle \ operatornév {arcosh} u \ pm \ operatornév {arcosh} v = \ operatornév {arcosh} \ left (uv \ pm {\ sqrt {(u^{2} -1) (v^{2} -1 )}}\jobb)}$

${\ displaystyle \ operatornév {artanh} u \ pm \ operatornév {artanh} v = \ operatornév {artanh} \ bal ({\ frac {u \ pm v} {1 \ pm uv}} \ jobb)}$

${\ displaystyle \ operatornév {arcoth} u \ pm \ operatornév {arcoth} v = \ operatornév {arcoth} \ bal ({\ frac {1 \ pm uv} {u \ pm v}} \ jobb)}$

${\ displaystyle {\ begin {aligned} \ operatnev -1)}} \ jobb) \\ & = \ operatornév {arcosh} \ left (v {\ sqrt {1+u^{2}}}+u {\ sqrt {v^{2} -1}} \ jobb) \ end {igazítva}}}$

Más identitások

${\ displaystyle {\ begin {aligned} 2 \ operatornév {arcosh} x & = \ operatornév {arcosh} (2x^{2} -1) & \ quad {\ hbox {for}} x \ geq 1 \\ 4 \ operatnev {arcosh} x & = \ operatornév {arcosh} (8x^{4} -8x^{2} +1) & \ quad {\ hbox {for}} x \ geq 1 \\ 2 \ operatorname {arsinh} x & = \ operatornév {arcosh} (2x^{2} +1) & \ quad {\ hbox {for}} x \ geq 0 \\ 4 \ operatorname {arsinh} x & = \ operatornév {arcosh} (8x^{4}+8x ^{2} +1) & \ quad {\ hbox {for}} x \ geq 0 \ end {aligned}}}$

${\ displaystyle \ ln (x) = \ operatornév {arcosh} \ left ({\ frac {x^{2} +1} {2x}} \ right) = \ operatorname {arsinh} \ left ({\ frac {x ^{2} -1} {2x}} \ jobb) = \ operatornév {artanh} \ bal ({\ frac {x^{2} -1} {x^{2} +1}} \ jobb)}$

A hiperbolikus és inverz hiperbolikus függvények összetétele

${\ displaystyle {\ begin {aligned} & \ sinh (\ operatornév {arcosh} x) = {\ sqrt {x^{2} -1}} \ quad {\ text {for}} \ quad | x |> 1 \\ & \ sinh (\ operatornév {artanh} x) = {\ frac {x} {\ sqrt {1 -x^{2}}}} \ quad {\ text {for}} \ quad -1 <x < 1 \\ & \ cosh (\ operatornév {arsinh} x) = {\ sqrt {1+x^{2}}} \\ & \ cosh (\ operatornév {artanh} x) = {\ frac {1} {\ sqrt {1 -x^{2}}}} \ quad {\ text {for}} \ quad -1 <x <1 \\ & \ tanh (\ operatornév {arsinh} x) = {\ frac {x} { \ sqrt {1+x^{2}}}} \\ & \ tanh (\ operatornév {arcosh} x) = {\ frac {\ sqrt {x^{2} -1}} {x}} \ quad { \ text {for}} \ quad | x |> 1 \ end {aligned}}}$

Inverz hiperbolikus és trigonometrikus függvények összetétele

${\ displaystyle \ operatornév {arsinh} \ left (\ tan \ alpha \ right) = \ operatorname {artanh} \ left (\ sin \ alpha \ right) = \ ln \ left ({\ frac {1+ \ sin \ alpha } {\ cos \ alpha}} \ jobb) = \ pm \ operatornév {arcosh} \ bal ({\ frac {1} {\ cos \ alpha}} \ jobb)}$

${\ displaystyle \ ln \ left (\ left | \ tan \ alpha \ right | \ right) =-\ operatorname {artanh} \ left (\ cos 2 \ alpha \ right)}$

Konverziók

${\ displaystyle \ ln x = \ operatornév {artanh} \ left ({\ frac {x^{2} -1} {x^{2} +1}} right) = \ operatorname {arsinh} \ left ({ \ frac {x^{2} -1} {2x}} \ jobb) = \ pm \ operatornév {arcosh} \ bal ({\ frac {x^{2} +1} {2x}} \ jobb)}$

${\ displaystyle \ operatornév {artanh} x = \ operatorname {arsinh} \ bal ({\ frac {x} {\ sqrt {1-x^{2}}}} \ jobb) = \ pm \ operatornév {arcosh} \ bal ({\ frac {1} {\ sqrt {1-x^{2}}}} \ jobb)}$

${\ displaystyle \ operatornév {arsinh} x = \ operatornév {artanh} \ bal ({\ frac {x} {\ sqrt {1+x^{2}}}} \ jobb) = \ pm \ operatornév {arcosh} \ bal ({\ sqrt {1+x^{2}}} \ jobb)}$

${\ displaystyle \ operatnev bal ({\ frac {\ sqrt {x^{2} -1}} {x}} \ jobb) \ jobb |}$

Származékok

${\ displaystyle {\ begin {aligned} {\ frac {d} {dx}} \ operatorname {arsinh} x & {} = {\ frac {1} {\ sqrt {x^{2} +1}}}, { \ text {for all real}} x \\ {\ frac {d} {dx}} \ operatornév {arcosh} x & {} = {\ frac {1} {\ sqrt {x^{2} -1}}} , {\ text {for all real}} x> 1 \\ {\ frac {d} {dx}} \ operatorname {artanh} x & {} = {\ frac {1} {1-x^{2}}} , {\ text {for all real}} | x | <1 \\ {\ frac {d} {dx}} \ operatorname {arcoth} x & {} = {\ frac {1} {1-x^{2} }}, {\ text {for all real}} | x |> 1 \\ {\ frac {d} {dx}} \ operatorname {arsech} x & {} = {\ frac {-1} {x {\ sqrt {1-x^{2}}}}}, {\ text {for all real}} x \ in (0,1) \\ {\ frac {d} {dx}} \ operatorname {arcsch} x & {} = {\ frac {-1} {| x | {\ sqrt {1+x^{2}}}}}, {\ text {minden valós}} x {\ text {, kivéve}} 0 \\\ vége {igazítva}}}$

Példa a differenciálásra: legyen θ = arsinh x , tehát (ahol sinh ² θ = (sinh θ ) ² ):

${\ displaystyle {\ frac {d \, \ operatornév {arsinh} x} {dx}} = {\ frac {d \ theta} {d \ sinh \ theta}} = {\ frac {1} {\ cosh \ theta }} = {\ frac {1} {\ sqrt {1+ \ sinh ^{2} \ theta}}} = {\ frac {1} {\ sqrt {1+x ^{2}}}}.}$

Sorozatbővítések

Bővítő sorozatok beszerezhetők a fenti funkciókhoz:

${\ displaystyle {\ begin {aligned} \ operatornév {arsinh} x & = x- \ left ({\ frac {1} {2}} \ right) {\ frac {x^{3}} {3}}+\ bal ({\ frac {1 \ cdot 3} {2 \ cdot 4}} \ jobb) {\ frac {x^{5}} {5}}-\ bal ({\ frac {1 \ cdot 3 \ cdot 5 } {2 \ cdot 4 \ cdot 6}} \ right) {\ frac {x^{7}} {7}} \ pm \ cdots \\ & = \ sum _ {n = 0}^{\ infty} \ bal ({\ frac {(-1)^{n} (2n)!} {2^{2n} (n!)^{2}}} \ jobb) {\ frac {x^{2n+1}} {2n+1}}, \ qquad \ left | x \ right | <1 \ end {aligned}}}$

${\ displaystyle {\ begin {aligned} \ operatornév {arcosh} x & = \ ln (2x)-\ left (\ left ({\ frac {1} {2}} \ right) {\ frac {x^{-2 }} {2}}+\ bal ({\ frac {1 \ cdot 3} {2 \ cdot 4}} \ jobb) {\ frac {x^{-4}} {4}}+\ bal ({\ frac {1 \ cdot 3 \ cdot 5} {2 \ cdot 4 \ cdot 6}} \ right) {\ frac {x^{-6}} {6}}+\ cdots \ right) \\ & = \ ln (2x)-\ összeg _ {n = 1}^{\ infty} \ bal ({\ frac {(2n)!} {2^{2n} (n!)^{2}}} \ jobb) {\ frac {x^{-2n}} {2n}}, \ qquad \ left | x \ right |> 1 \ end {aligned}}}$

${\ displaystyle {\ begin {aligned} \ operatornév {artanh} x & = x+{\ frac {x^{3}} {3}}+{\ frac {x^{5}} {5}}+{\ frac {x^{7}} {7}}+\ cdots \\ & = \ sum _ {n = 0}^{\ infty} {\ frac {x^{2n+1}} {2n+1}}, \ qquad \ left | x \ right | <1 \ end {igazított}}}$

${\ displaystyle {\ begin {aligned} \ operatorname {arcsch} x = \ operatorname {arsinh} {\ frac {1} {x}} & = x^{-1}-\ left ({\ frac {1} { 2}} \ jobb) {\ frac {x^{-3}} {3}}+\ bal ({\ frac {1 \ cdot 3} {2 \ cdot 4}} \ jobb) {\ frac {x^ {-5}} {5}}-\ bal ({\ frac {1 \ cdot 3 \ cdot 5} {2 \ cdot 4 \ cdot 6}} \ jobb) {\ frac {x^{-7}} { 7}} \ pm \ cdots \\ & = \ sum _ {n = 0}^{\ infty} \ left ({\ frac {(-1)^{n} (2n)!} {2^{2n}) (n!)^{2}}} \ jobb) {\ frac {x^{-(2n+1)}} {2n+1}}, \ qquad \ left | x \ right |> 1 \ end {igazítva }}}$

${\ displaystyle {\ begin {aligned} \ operatornév {arsech} x = \ operatornév {arcosh} {\ frac {1} {x}} & = \ ln {\ frac {2} {x}}-\ left (\ bal ({\ frac {1} {2}} \ jobb) {\ frac {x^{2}} {2}}+\ bal ({\ frac {1 \ cdot 3} {2 \ cdot 4}} \ jobb) {\ frac {x^{4}} {4}}+\ bal ({\ frac {1 \ cdot 3 \ cdot 5} {2 \ cdot 4 \ cdot 6}} \ jobb) {\ frac {x ^{6}} {6}}+\ cdots \ right) \\ & = \ ln {\ frac {2} {x}}-\ sum _ {n = 1}^{\ infty} \ left ({\ frac {(2n)!} {2^{2n} (n!)^{2}}} \ right) {\ frac {x^{2n}} {2n}}, \ qquad 0 <x \ leq 1 \ vége {igazítva}}}$

${\ displaystyle {\ begin {aligned} \ operatornév {arcoth} x = \ operatornév {artanh} {\ frac {1} {x}} & = x^{-1}+{\ frac {x^{-3} } {3}}+{\ frac {x^{-5}} {5}}+{\ frac {x^{-7}} {7}}+\ cdots \\ & = \ sum _ {n = 0}^{\ infty} {\ frac {x^{-(2n+1)}} {2n+1}}, \ qquad \ left | x \ right |> 1 \ end {aligned}}}$

Aszimptotikus sor a arsinh x adják

${\ displaystyle \ operatornév {arsinh} x = \ ln (2x)+\ összeg \ korlátok _ {n = 1}^{\ infty} {\ left ({-1} \ right)^{n-1} {\ frac {\ balra ({2n-1} \ jobbra) !!} {2n \ balra ({2n} \ jobbra) !!}}} {\ frac {1} {x^{2n}}}}$

Főbb értékek a komplex síkban

Az inverz hiperbolikus függvények összetett változó függvényekként többértékű függvények , amelyek analitikusak , kivéve véges számú ponton. Egy ilyen funkciót, ez a közös, hogy meghatározza egy legfőbb értéke , amely egyetlen értékes analitikus függvény, amely egybeesik egy specifikus ága a többértékű függvény, mint egy domént, amely a komplex síkban , amelyben véges számú ívek (általában fele vonalak vagy vonalszakaszok ) eltávolításra került. Ezek az ívek nevezzük ág darabok . Az ág meghatározásához, azaz annak meghatározásához, hogy a többértékű függvény melyik értékét vesszük figyelembe minden pontban, általában egy adott ponton határozzuk meg, és az értéket mindenütt a főérték meghatározásának tartományában vonjuk le analitikus folytatással . Ha lehetséges, jobb a főértéket közvetlenül meghatározni, anélkül, hogy az analitikus folytatásra hivatkoznánk.

Például a négyzetgyök esetében a főértéket a négyzetgyök határozza meg, amelynek pozitív valós része van . Ez egyetlen értékű analitikai függvényt határoz meg, amelyet mindenhol definiálnak, kivéve a változók nem pozitív valós értékeit (ahol a két négyzetgyöknek nulla valós része van). A négyzetgyök függvény ezen fő értékét az alábbiakban jelöljük . Hasonlóképpen, a logaritmus főértékét, amelyet a következőkben jelölünk , úgy definiálunk, mint azt az értéket, amelyhez a képzeletbeli rész rendelkezik a legkisebb abszolút értékkel. Mindenhol definiálva van, kivéve a változó nem pozitív valós értékeit, amelyeknél a logaritmus két különböző értéke eléri a minimumot. ${\ displaystyle {\ sqrt {x}}}$${\ displaystyle \ operatornév {Napló}}$

Minden inverz hiperbolikus függvény esetében a főérték a négyzetgyök és a logaritmusfüggvény főértékei alapján határozható meg. Bizonyos esetekben azonban a § Definíciók logaritmus szerinti képletei nem adnak meg helyes főértéket, mivel túl kicsi és egy esetben nem kapcsolódó definíciós tartományt adnak .

Az inverz hiperbolikus szinusz főértéke

Az inverz hiperbolikus szinusz főértékét a

${\ displaystyle \ operatornév {arsinh} z = \ operatornév {Napló} (z+{\ sqrt {z^{2} +1}} \,) \ ,.}$

A négyzetgyök argumentuma nem pozitív valós szám, akkor és csak akkor, ha z a képzeletbeli tengely [ i , + i ∞) és ( -i ∞, -i ] intervallumának egyikébe tartozik . Ha a a logaritmus valós, akkor pozitív. Így ez a képlet meghatározza az arsinh főértékét, elágazásokkal [ i , + i ∞) és ( - i ∞, - i ] . Ez optimális, mivel az ágvágásoknak össze kell kapcsolódniuk az egyes szám i és - i végtelenségig.

Az inverz hiperbolikus koszinusz főértéke

A § Az inverz hiperbolikus koszinuszra vonatkozó, az Inverz hiperbolikus koszinusz képlet nem kényelmes, mivel a logaritmus és a négyzetgyök főértékeihez hasonlóan az arcosh főértéke nem lenne definiálva a képzeletbeli z esetében . Ezért a négyzetgyököt faktorizálni kell, ami ahhoz vezet

${\ displaystyle \ operatornév {arcosh} z = \ operatornév {Log} (z+{\ sqrt {z+1}} {\ sqrt {z-1}} \,) \ ,.}$

A négyzetgyökök főértékei mind definiáltak, kivéve, ha z a valós intervallumhoz tartozik (−∞, 1] . Ha a logaritmus argumentuma valós, akkor z valós és ugyanaz az előjele. Így a fenti képlet az arcosh fő értékét határozza meg a valós intervallumon kívül (−∞, 1] , amely így az egyedi ágvágás .

Az inverz hiperbolikus érintő és kotangens fő értékei

A § Definíciók logaritmusban megadott képletek azt sugallják

${\ displaystyle {\ begin {aligned} \ operatornév {artanh} z & = {\ frac {1} {2}} \ operatornév {Log} \ bal ({\ frac {1+z} {1-z}} \ jobb ) \\\ operatornév {arcoth} z & = {\ frac {1} {2}} \ operatornév {Log} \ balra ({\ frac {z+1} {z-1}} \ jobb) \ end {aligned} }}$

az inverz hiperbolikus érintő és kotangens fő értékeinek meghatározásához. Ezekben a képletekben a logaritmus argumentuma akkor és csak akkor valós, ha z valós. Artanh esetében ez az argumentum a valós intervallumban van (−∞, 0] , ha z vagy (−∞, −1] vagy [1, ∞) . Arcoth esetén a logaritmus argumentuma (−∞ , 0] , akkor és csak akkor, ha z a [−1, 1] valós intervallumhoz tartozik .

Ezért ezek a képletek kényelmes főértékeket határoznak meg, amelyekhez az elágazások (−∞, −1] és [1, ∞) az inverz hiperbolikus érintő esetében, és [−1, 1] az inverz hiperbolikus kotangens esetében.

Figyelembe véve a jobb számszerű értékelést az ágvágások közelében, egyes szerzők a főértékek alábbi definícióit használják, bár a második egy eltávolítható szingularitást vezet be z = 0 -nál . A két meghatározását eltérnek a valós értékek az . Azok az különböznek a valódi értékek az . ${\ displaystyle \ operatornév {artanh}}$${\ displaystyle z}$${\ displaystyle z> 1}$${\ displaystyle \ operatornév {arcoth}}$${\ displaystyle z}$${\ displaystyle z \ in [0,1]}$

${\ displaystyle {\ begin {aligned} \ operatornév {artanh} z & = {\ tfrac {1} {2}} \ operatorname {Log} \ bal ({1+z} \ jobb)-{\ tfrac {1} { 2}} \ operatornév {Napló} \ balra ({1-z} \ jobbra) \\\ operatornév {arcoth} z & = {\ tfrac {1} {2}} \ operatornév {Log} \ balra ({1+ { \ frac {1} {z}}} \ jobb)-{\ tfrac {1} {2}} \ operatornév {Log} \ bal ({1-{\ frac {1} {z}}} \ jobb) \ vége {igazítva}}}$

Az inverz hiperbolikus kozekáns fő értéke

Az inverz hiperbolikus kozekáns esetében a főérték a következő

${\ displaystyle \ operatornév {arcsch} z = \ operatorname {Log} \ left ({\ frac {1} {z}}+{\ sqrt {{\ frac {1} {z^{2}}}+1} }\,\jobb)}$.

Ezt akkor határozzuk meg, ha a logaritmus és a négyzetgyök argumentumai nem nem pozitív valós számok. A négyzetgyök főértékét tehát a képzeletbeli egyenes [ - i , i ] intervallumán kívül határozzuk meg . Ha a logaritmus argumentuma valós, akkor z nem nulla valós szám, és ez azt jelenti, hogy a logaritmus argumentuma pozitív.

Így a fő érték meghatározása a fenti képlet által kívül ága vágott , amely az intervallum [- i , i ] a képzeletbeli vonal.

A Z = 0 , van egy szinguláris pont, amely benne van a ág vágás.

Az inverz hiperbolikus szekáns fő értéke

Itt is, mint az inverz hiperbolikus koszinusz esetében, a négyzetgyököt kell faktorizálnunk. Ez adja a fő értéket

${\ displaystyle \ operatornév {arsech} z = \ operatornév {Log} \ left ({\ frac {1} {z}}+{\ sqrt {{\ frac {1} {z}}+1}} \, { \ sqrt {{\ frac {1} {z}}-1}} \ jobb).}$

Ha egy négyzetgyök argumentuma valós, akkor z valós, és ebből következik, hogy a négyzetgyök mindkét fő értéke definiált, kivéve, ha z valós és az (−∞, 0] és [1, intervallumok egyikéhez tartozik) +∞) . Ha a logaritmus argumentuma valós és negatív, akkor z is valós és negatív. Ebből következik, hogy a fő értéke arsech jól meghatározott, a fenti képlet által kívül két ága vágások , a valós intervallumok (-∞, 0] és [1, + ∞) .

A Z = 0 , van egy szinguláris pont, amely tartalmazza az egyik ág vágások.

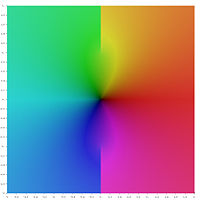
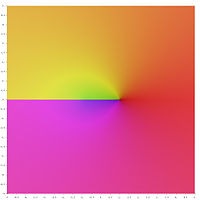
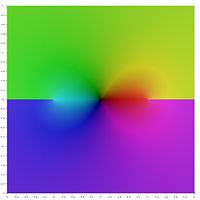
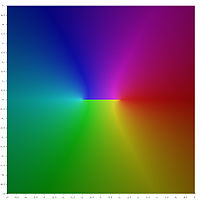
Grafikus ábrázolás

Az inverz hiperbolikus függvények fő értékeinek következő grafikus ábrázolásában az ágvágások a szín megszakításaként jelennek meg. Az a tény, hogy az egész ágvágás megszakításként jelenik meg, azt mutatja, hogy ezeket a főértékeket nem lehet kiterjeszteni a nagyobb területeken meghatározott analitikai függvényekre. Más szóval, a fent meghatározott ágvágások minimálisak.

Lásd még

• Összetett logaritmus
• Hiperbolikus szekáns eloszlás
• ISO 80000-2
• Inverz hiperbolikus függvények integráljainak listája

Hivatkozások

Bibliográfia

• Herbert Busemann és Paul J. Kelly (1953) Projektív geometria és projektív metrika , 207. oldal, Academic Press .

Külső linkek

• "Inverz hiperbolikus függvények" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]