Terület - Area

Terület
Gyakori szimbólumok	A
SI egység	Négyzetméter [m 2 ]
Az SI alapegységek	1  m 2
Dimenzió	${\ displaystyle {\ mathsf {L}}^{2}}$

A terület az a mennyiség, amely egy kétdimenziós régió , alakzat vagy sík lamina kiterjedését fejezi ki a síkban . A felület az analógja egy háromdimenziós objektum kétdimenziós felületén . A terület alatt fel lehet érteni az adott vastagságú anyagmennyiséget, amely szükséges lenne az alakzat modelljének kialakításához, vagy azt a festékmennyiséget, amely szükséges a felület egyetlen réteggel történő lefedéséhez. Ez egy görbe hosszának (egydimenziós fogalom) vagy egy szilárd anyag térfogatának (háromdimenziós fogalom) kétdimenziós analógja .

Az alakzat területét úgy lehet mérni, hogy összehasonlítjuk az alakzatot egy rögzített méretű négyzetekkel . A nemzetközi mértékegység -rendszerben (SI) a szabványos területegység a négyzetméter (m ² -ként írva ), amely egy négyzet területe, amelynek oldalai egy méter hosszúak. Egy három négyzetméter alapterületű alakzatnak ugyanolyan területe lenne, mint három ilyen négyzetnek. A matematikában az egység négyzetet úgy határozták meg, hogy területe egy, más alakzat vagy felület területe pedig dimenzió nélküli valós szám .

Az egyszerű formák, például háromszögek , téglalapok és körök számos jól ismert képlettel rendelkeznek . Ezekkel a képletekkel bármelyik sokszög területe megtalálható a sokszög háromszögekre osztásával . Ívelt szegéllyel rendelkező alakzatok esetén általában számításra van szükség a terület kiszámításához. Valójában a síkfigurák területének meghatározásának problémája fő oka volt a számítás történelmi fejlődésének .

A szilárd forma, mint egy gömb , kúp, vagy henger, a terület határoló felülete az úgynevezett felülete . Az egyszerű alakzatok felületének képleteit az ókori görögök számították ki , de egy bonyolultabb alakzat felületének kiszámítása általában többváltozós számítást igényel .

A terület fontos szerepet játszik a modern matematikában. Amellett, hogy a terület nyilvánvaló fontosságú a geometriában és a számításban, a terület összefügg a lineáris algebrai determinánsok meghatározásával , és a differenciálgeometria felületeinek alapvető tulajdonsága . Az elemzés során a sík egy részhalmazának területét Lebesgue -mérték segítségével határozzuk meg , bár nem minden részhalmaz mérhető. Általában a területet a magasabb matematikában a kétdimenziós régiók térfogatának különleges esetének tekintik.

A terület axiómák használatával határozható meg, meghatározva azt a valós számok halmazához tartozó bizonyos síkfigurák gyűjteményének függvényében. Bizonyítható, hogy létezik ilyen funkció.

Formális meghatározás

A "terület" alatt definiálható megközelítés axiómákon keresztül történik . A "terület" egy speciális típusú síkfigurák (gyűjthető halmazok) M gyűjteményétől a valós számok halmazáig terjedő függvényként definiálható, amely megfelel a következő tulajdonságoknak:

• Minden S az M , a ( S ) ≥ 0.
• Ha S és T M -ben vannak, akkor S ∪ T és S ∩ T is , valamint a ( S ∪ T ) = a ( S ) + a ( T ) - a ( S ∩ T ).
• Ha S és T vannak M a S ⊆ T , majd T - S van M és egy ( T - S ) = a ( T ) - a ( S ).
• Ha egy S halmaz M -ben van, és S egybevág T -vel, akkor T is M -ben van, és a ( S ) = a ( T ).
• Minden R téglalap M -ben van . Ha a téglalap hossza h és szélessége K , majd a ( R ) = hk .
• Legyen Q egy halmaz, amely két S és T lépéstartomány között van . Egy lépés régió van kialakítva egy véges unió szomszédos téglalapok nyugvó közös bázis, azaz S ⊆ Q ⊆ T . Ha létezik olyan egyedi c szám , hogy a ( S ) ≤ c ≤ a ( T ) minden ilyen S és T lépésrégióban , akkor a ( Q ) = c .

Bizonyítható, hogy létezik ilyen területfüggvény.

Egységek

Minden hosszegységnek megfelelő területegysége van, nevezetesen az adott oldalhosszúságú négyzet területe. Így a területek négyzetméter (m ² ), négyzetcentiméter (cm ² ), négyzetmilliméter (mm ² ), négyzetkilométer (km ² ), négyzetláb (ft ² ), négyzetméter (yd ² ), négyzet mérföld mérhetők (mi ² ), és így tovább. Algebrai értelemben ezeket az egységeket úgy tekinthetjük, mint a megfelelő hosszegységek négyzeteit .

Az SI területegység a négyzetméter, amely SI származtatott egységnek minősül .

Konverziók

Az 1 méter hosszúságú és szélességű négyzet területének kiszámítása a következő lenne:

1 méter × 1 méter = 1 m ²

és így egy téglalap, amelynek különböző oldalai (mondjuk hossza 3 méter, szélessége 2 méter), négyzetméteres területtel rendelkezik, amely a következőképpen számítható ki:

3 méter × 2 méter = 6 m ² . Ez 6 millió négyzetmilliméternek felel meg. További hasznos konverziók:

• 1 négyzetkilométer = 1 000 000 négyzetméter
• 1 négyzetméter = 10 000 négyzetcentiméter = 1 000 000 négyzetmilliméter
• 1 négyzetcentiméter = 100 négyzetmilliméter.

Nem metrikus egységek

Nem metrikus egységekben a két négyzetegység közötti konverzió a megfelelő hosszúságú egységek közötti konverzió négyzete .

1 láb = 12 hüvelyk ,

a négyzetláb és a négyzet hüvelyk közötti kapcsolat az

1 négyzetláb = 144 négyzet hüvelyk,

ahol 144 = 12 ² = 12 × 12. Hasonlóan:

• 1 négyzetméter = 9 négyzetméter
• 1 négyzet mérföld = 3 097 600 négyzetméter = 27 878 ​​400 négyzetméter

Ezenkívül a konverziós tényezők a következők:

• 1 négyzethüvelyk = 6,4516 négyzetcentiméter
• 1 négyzetláb = 0,092 903 04 négyzetméter
• 1 négyzetméteres udvar = 0,836 127 36 négyzetméter
• 1 négyzet mérföld = 2,589 988 110 336 négyzetkilométer

Más egységek, beleértve a történelmi

A területen több más közös egység is létezik. Az are volt a metrikus rendszer eredeti területegysége , a következőkkel:

• 1 are = 100 négyzetméter

Habár az areák használaton kívül estek, a hektárt még mindig gyakran használják a földek mérésére:

• 1 hektár = 100 aré = 10 000 négyzetméter = 0,01 négyzetkilométer

Egyéb nem gyakori metrikus területegységek közé tartozik a tetrád , a hektár és a számtalan .

A hektárt általában földterületek mérésére is használják, ahol

• 1 hektár = 4840 négyzetméter = 43 560 négyzetméter.

Egy hektár a hektár körülbelül 40% -a.

Az atomskálán a területet pajtaegységekben mérik , úgy, hogy:

• 1 pajta = 10 ⁻²⁸ négyzetméter.

Az istállót általában a nukleáris fizika kölcsönhatásának keresztmetszeti területének leírására használják .

A India ,

• 20 dhurki = 1 dhur
• 20 dhur = 1 khatha
• 20 khata = 1 bigha
• 32 khata = 1 hold

Történelem

Kör terület

Az 5. században BCE, Hippokratész, Chios volt az első, aki azt mutatják, hogy a terület egy lemez (bezárt területen egy kör) négyzetével arányos az átmérője, részeként a négyszögjel a lune Hippokratész , de nem nem azonosítja az arányosság állandóját . Cnidusi Eudoxus , szintén i. E. 5. században, azt is megállapította, hogy a korong területe arányos a sugár négyzetével.

Ezt követően az Euklidész elemei I. könyv a kétdimenziós ábrák közötti területek egyenlőségével foglalkozott. Arkhimédész matematikus az euklideszi geometria eszközeivel mutatta be, hogy a Kör mérése című könyvében megmutatja, hogy a körön belüli terület egyenlő egy derékszögű háromszög területével, amelynek alapja a kör kerületének hossza, és magassága megegyezik a kör sugarával . (A kerülete 2 π r , a háromszög területe pedig a magasság fele a magassággal, így a korong π r ² területe lesz .) Archimedes közelítette a π értékét (és így az egység sugarú kör területét is) ) duplázási módszerével , amelyben egy szabályos háromszöget írt körbe, és feljegyezte annak területét, majd megduplázta az oldalak számát, hogy szabályos hatszöget kapjon , majd többször megduplázta az oldalak számát, amikor a sokszög területe egyre közelebb került ehhez a körből (és ugyanezt tette a körülírt sokszögekkel ).

Johann Heinrich Lambert svájci tudós 1761 -ben bebizonyította, hogy π , egy kör területének és négyzet sugarának aránya irracionális , vagyis nem egyenlő két egész szám hányadosával. 1794-ben Adrien-Marie Legendre francia matematikus bebizonyította, hogy π ² irracionális; ez is azt bizonyítja, hogy π irracionális. 1882 -ben Ferdinand von Lindemann német matematikus bebizonyította, hogy π transzcendentális (nem bármely racionális együtthatójú polinom -egyenlet megoldása ), megerősítve mind a Legendre , mind az Euler -féle feltételezést.

Háromszög terület

Az alexandriai Heron (vagy hős) megtalálta az úgynevezett Heron képletét a háromszög oldalára nézve, és bizonyíték található a CE 60 körül írt Metrica című könyvében . Felmerült, hogy Archimedes több mint két évszázaddal korábban ismerte a képletet, és mivel a Metrica az ókori világban rendelkezésre álló matematikai ismeretek gyűjteménye, lehetséges, hogy a képlet megelőzi a műben megadott hivatkozást.

499 -ben Aryabhata , egy nagyszerű matematikus - csillagász az indiai matematika és az indiai csillagászat klasszikus korából, egy háromszög területét az Aryabhatiya magasságának fele -fele arányában fejezte ki (2.6. Szakasz).

A kínaiak a görögöktől függetlenül felfedezték a Heronéval egyenértékű formulát. 1247 -ben jelent meg Shushu Jiuzhangban (" Matematikai értekezés kilenc szakaszban "), amelyet Qin Jiushao írt .

Négyszög terület

A 7. században Brahmagupta kifejlesztett egy képletet, amelyet ma Brahmagupta képletének neveznek, egy ciklikus négyszög ( egy körbe írt négyszög ) területének oldalait tekintve. 1842 -ben a német matematikusok, Carl Anton Bretschneider és Karl Georg Christian von Staudt egymástól függetlenül találtak egy képletet, amelyet Bretschneider képletének neveznek, bármely négyszög területére.

Általános sokszög terület

A fejlesztés a derékszögű koordináta-rendszerben a René Descartes a 17. században tette az a felügyelők formula a terület minden sokszög ismert vertex helyeken Gauss a 19. században.

Számítással meghatározott területek

A 17. század végén az integrálszámítás kifejlesztése olyan eszközöket biztosított, amelyek később bonyolultabb területek, például egy ellipszis és különböző ívelt háromdimenziós objektumok felületének kiszámításához használhatók .

Terület képletek

Sokszög képletek

Egy nem önmagát metsző ( egyszerű ) sokszög esetén, amelynek n csúcsának derékszögű koordinátái ( i = 0, 1, ..., n -1) ismertek, a területet a felmérő képlete adja meg : ${\ displaystyle (x_ {i}, y_ {i})}$

${\ displaystyle A = {\ frac {1} {2}} {\ Biggl \ vert} \ sum _ {i = 0}^{n-1} (x_ {i} y_ {i+1} -x_ {i +1} y_ {i}) {\ Biggr \ vert}}$

ahol amikor i = n -1, akkor i +1 n modulusként fejeződik ki, és így 0 -ra utal.

Téglalapok

A legalapvetőbb területképlet a téglalap területének képlete . Adott egy l hosszúságú és w szélességű téglalap, a terület képlete a következő:

A = lw  (téglalap).

Vagyis a téglalap területe a hosszúság és a szélesség szorzata. Mint egy különleges eset, mivel L = W esetén egy négyzet alakú, a terület egy négyzet oldalhosszúságú s az a következő képlet adja:

A = s ²  (négyzet).

A téglalap területének képlete közvetlenül a terület alapvető tulajdonságaiból következik, és néha definíciónak vagy axiómának tekintik . Másrészről, ha a geometriát az aritmetika előtt fejlesztik ki , akkor ezzel a képlettel lehet meghatározni a valós számok szorzását .

Boncolás, paralelogramma és háromszög

A terület többi egyszerű formulája a boncolás módszeréből következik . Ez magában foglalja a vágás egy alak darabokra, amelyek területén kell összefoglalni , hogy a terület az eredeti alakját.

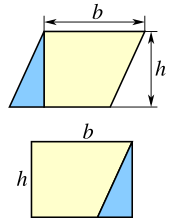
Például bármely paralelogramma felosztható trapézra és derékszögű háromszögre , amint azt a bal oldali ábra mutatja. Ha a háromszöget áthelyezzük a trapéz másik oldalára, akkor a kapott ábra egy téglalap. Ebből következik, hogy a paralelogramma területe megegyezik a téglalap területével:

A = bh  (paralelogramma).

Ugyanaz a paralelogramma azonban átlós mentén két egybevágó háromszögre is vágható , amint azt a jobb oldali ábra mutatja. Ebből következik, hogy minden háromszög területe fele a paralelogramma területének:

${\ displaystyle A = {\ frac {1} {2}} bh}$  (háromszög).

Hasonló érvekkel lehet keresni a trapéz területképleteit , valamint a bonyolultabb sokszögeket .

Ívelt formák területe

Körök

A kör területének képlete (pontosabban kör vagy zárt terület vagy a lemez területe ) hasonló módszerre épül. Ha egy r sugarú kört adunk meg , akkor a kört szektorokra lehet felosztani , amint azt a jobb oldali ábra mutatja. Mindegyik szektor megközelítőleg háromszög alakú, és a szektorok átrendezhetők, hogy megközelítő paralelogrammát képezzenek. Ennek a paralelogrammának a magassága r , a szélessége pedig a kör kerületének fele , vagy π r . Így a kör teljes területe π r ² :

A = π r ²  (kör).

Bár a képletben használt boncolás csak hozzávetőleges, a hiba egyre kisebb lesz, ahogy a kört egyre több szektorra osztják szét. A közelítő paralelogrammák területeinek határa pontosan π r ² , ami a kör területe.

Ez az érv valójában a számítás ötleteinek egyszerű alkalmazása . Az ókorban a kimerülés módszerét hasonló módon használták a kör területének megtalálásához, és ezt a módszert ma már az integrálszámítás előfutárának ismerik el . A modern módszerek segítségével a kör területe kiszámítható egy meghatározott integrál segítségével :

${\ displaystyle A \; = \; 2 \ int _ {-r}^{r} {\ sqrt {r^{2} -x^{2}}} \, dx \; = \; \ pi r^ {2}.}$

Ellipszisek

Az ellipszissel zárt terület képlete összefügg a kör képletével; egy ellipszis félig-major és félig kisebb tengelyek x és y a képlet a következő:

${\ displaystyle A = \ pi xy.}$

Felszíni terület

A felület alapformuláinak többsége a felületek vágásával és lelapításával kapható. Például, ha egy henger (vagy bármilyen prizma ) oldalfelületét hosszában vágják, akkor a felület téglalap alakúra simítható. Hasonlóképpen, ha egy kúp oldala mentén vágást végeznek, akkor az oldalfelületet egy kör szektorává lehet lapítani, és a kapott területet kiszámítani.

A gömb felületének képletét nehezebb levezetni: mivel a gömb nem nulla Gauss -görbületű , nem lehet lelapítani. A gömb felületének képletét először Archimedes szerezte meg a gömbről és a hengerről című munkájában . A képlet a következő:

A = 4 πr ²  (gömb),

ahol r a gömb sugara. A kör területének képletéhez hasonlóan ennek a képletnek minden származtatása eredendően a számításhoz hasonló módszereket használ .

Általános képletek

2 dimenziós ábrák területei

• A háromszög : (ahol B jelentése bármely oldalán, és h jelentése a távolság a vonalon, amelyen a B hazugság a másik csúcsa a háromszög). Ez a képlet használható, ha ismert a h magasság . Ha a három oldal hossza ismert, akkor Heron képletét lehet használni: ahol a , b , c a háromszög oldalai, és a kerülete fele. Ha egy szög és annak két mellékelt oldala meg van adva, akkor a terület az, ahol C a megadott szög, és a és b a mellékelt oldalai. Ha a háromszöget egy koordináta síkon ábrázoljuk, akkor mátrix használható, és egyszerűsítve lesz az abszolút értékére . Ezt a képletet cipőfűző képletnek is nevezik, és egy egyszerű módja annak, hogy megoldja a koordináta háromszög területét a 3 (x ₁ , y ₁ ) , (x ₂ , y ₂ ) és (x ₃ , y ₃ ) . A cipőfűző képlet felhasználható más sokszögek területeinek megkeresésére is, ha a csúcsaik ismertek. A koordináta háromszög másik megközelítése a számítás használata a terület megkereséséhez.${\ displaystyle {\ tfrac {1} {2}} Bh}$${\ displaystyle {\ sqrt {s (sa) (sb) (sc)}}}$${\ displaystyle s = {\ tfrac {1} {2}} (a+b+c)}$${\ displaystyle {\ tfrac {1} {2}} ab \ sin (C)}$${\ displaystyle {\ tfrac {1} {2}} (x_ {1} y_ {2}+x_ {2} y_ {3}+x_ {3} y_ {1} -x_ {2} y_ {1}- x_ {3} y_ {2} -x_ {1} y_ {3})}$
• Egy egyszerű poligon épített egy rács egyenlő távolságtartó pont (azaz, pontok egész koordinátákat) úgy, hogy az összes a poligon csúcsai rácspontok: , ahol i az a szám, rácspontok a sokszög belsejében, és b jelentése a száma határpontok . Ezt az eredményt Pick -tételnek nevezik .${\ displaystyle i+{\ frac {b} {2}}-1}$

Terület számításban

• A terület közötti pozitív értékű görbe és a vízszintes tengely, mért két érték között egy és b (b úgy definiáljuk, mint a nagyobb a két érték) a vízszintes tengelyen, az által adott integrál egy a b a a funkciót, amely a görbét ábrázolja:

${\ displaystyle A = \ int _ {a}^{b} f (x) \, dx.}$

• A terület közötti grafikonok a két funkció megegyezik az integrál egy függvény , F ( x ), mínusz az integrál a többi funkció, g ( x ):

${\ displaystyle A = \ int _ {a}^{b} (f (x) -g (x)) \, dx,}$hol a nagyobb y-értékű görbe.${\ displaystyle f (x)}$

• A poláris koordinátákban kifejezett függvény által határolt terület :${\ displaystyle r = r (\ théta)}$

${\ displaystyle A = {1 \ over 2} \ int r^{2} \, d \ theta.}$

• A paraméteres görbe által határolt területet végpontokkal az egyenes integrálok adják meg :${\ displaystyle {\ vec {u}} (t) = (x (t), y (t))}$${\ displaystyle {\ vec {u}} (t_ {0}) = {\ vec {u}} (t_ {1})}$

${\ displaystyle \ oint _ {t_ {0}}^{t_ {1}} x {\ dot {y}} \, dt =-\ oint _ {t_ {0}}^{t_ {1}} y { \ dot {x}} \, dt = {1 \ over 2} \ oint _ {t_ {0}}^{t_ {1}} (x {\ dot {y}}-y {\ pont {x}} ) \, dt}$

vagy a z -összetevője

${\ displaystyle {1 \ over 2} \ oint _ {t_ {0}}^{t_ {1}} {\ vec {u}} \ times {\ dot {\ vec {u}}} \, dt.}$

(Részletekért lásd Green tétele § Területszámítás .) Ez a planiméter mechanikus eszköz elve .

Korlátos terület két másodfokú függvény között

Ahhoz, hogy megtaláljuk a határolt területet két másodfokú függvény között , kivonjuk az egyiket a másikból , hogy a különbséget úgy írjuk fel

${\ displaystyle f (x) -g (x) = ax^{2}+bx+c = a (x- \ alfa) (x- \ beta)}$

ahol f ( x ) a másodfok felső határa, és g ( x ) a másodfok alsó határa. Határozza meg a diszkriminancia a F ( x ) - g ( x ), mint

${\ displaystyle \ Delta = b^{2} -4ac.}$

A két függvény grafikonja közötti integrálképlet egyszerűsítésével (a fenti szakaszban megadottak szerint) és Vieta képletének felhasználásával

${\ displaystyle A = {\ frac {\ Delta {\ sqrt {\ Delta}}} {6a^{2}}} = {\ frac {a} {6}} (\ beta -\ alfa)^{3} , \ qquad a \ neq 0.}$

A fentiek érvényesek maradnak, ha az egyik határoló függvény lineáris, nem másodfokú.

3 dimenziós figurák felülete

• Cone : , ahol R jelentése a sugár a kör alapú, és h jelentése a magassága. Ez átírható úgy is, hogy vagy ahol r a sugár, és l a kúp ferde magassága. az alapterület, míg a kúp oldalfelülete.${\ displaystyle \ pi r \ left (r+{\ sqrt {r^{2}+h^{2}}} \ jobb)}$${\ displaystyle \ pi r^{2}+\ pi rl}$${\ displaystyle \ pi r (r+l) \, \!}$${\ displaystyle \ pi r^{2}}$${\ displaystyle \ pi rl}$
• kocka : ahol s a hossza egy él.${\ displaystyle 6s^{2}}$
• henger : , ahol r a sugara egy bázis és H a magassága. A 2 r d -re is átírható , ahol d az átmérő.${\ displaystyle 2 \ pi r (r+h)}$${\ displaystyle \ pi}$${\ displaystyle \ pi}$
• prizma : 2B + Ph, ahol B egy bázis területe, P egy bázis kerülete, és h a prizma magassága.
• piramis : ahol B az alap területe, P az alap kerülete, és L a ferde hossza.${\ displaystyle B+{\ frac {PL} {2}}}$
• téglalap alapú hasáb : , ahol az a hossz, W a szélessége, és h a magassága.${\ displaystyle 2 (\ ell w+\ ell h+wh)}$${\ displaystyle \ ell}$

Általános képlet a felületre

A folytonosan differenciálható függvény grafikonjának felületének általános képlete, ahol és az xy-síkban egy sima határral rendelkező régió: ${\ displaystyle z = f (x, y),}$${\ displaystyle (x, y) \ in D \ alhalmaz \ mathbb {R} ^{2}}$${\ displaystyle D}$

${\ displaystyle A = \ iint _ {D} {\ sqrt {\ left ({\ frac {\ részleges f} {\ részleges x}} \ jobb)^{2}+\ bal ({\ frac {\ rész f } {\ részleges y}} \ jobb)^{2} +1}} \, dx \, dy.}$

Egy még általánosabb képlet a vektoros alakú paraméteres felület gráfjának azon területére, ahol a folyamatosan differenciálható vektorfüggvény : ${\ displaystyle \ mathbf {r} = \ mathbf {r} (u, v),}$${\ displaystyle \ mathbf {r}}$${\ displaystyle (u, v) \ in D \ alhalmaz \ mathbb {R} ^{2}}$

${\ displaystyle A = \ iint _ {D} \ balra | {\ frac {\ részleges \ mathbf {r}} {\ részleges u}} \ alkalommal {\ frac {\ részleges \ mathbf {r}} {\ rész v }} \ jobb | \, du \, dv.}$

Képletek listája

További gyakori képletek a területhez:

Alak	Képlet	Változók
Téglalap	${\ displaystyle A = ab}$
Háromszög	${\ displaystyle A = {\ frac {1} {2}} bh \, \!}$
Háromszög	${\ displaystyle A = {\ frac {1} {2}} ab \ sin (\ gamma) \, \!}$
Háromszög ( Heron képlet )	${\ displaystyle A = {\ sqrt {s (sa) (sb) (sc)}} \, \!}$	${\ displaystyle s = {\ tfrac {1} {2}} (a+b+c)}$
Egyenlő szárú háromszög	${\ displaystyle A = {\ frac {b} {4}} {\ sqrt {4a^{2} -c^{2}}}}$
Szabályos háromszög ( egyenlő oldalú háromszög )	${\ displaystyle A = {\ frac {\ sqrt {3}} {4}} a^{2} \, \!}$
Rombusz / sárkány	${\ displaystyle A = {\ frac {1} {2}} de}$
Paralelogramma	${\ displaystyle A = ah_ {a} \, \!}$
Trapéz	${\ displaystyle A = {\ frac {(a+c) h} {2}} \, \!}$
Szabályos hatszög	${\ displaystyle A = {\ frac {3} {2}} {\ sqrt {3}} a^{2} \, \!}$
Szabályos nyolcszög	${\ displaystyle A = 2 (1+{\ sqrt {2}}) a^{2} \, \!}$
Szabályos sokszög ( oldalak) ${\ displaystyle n}$	${\ displaystyle A = n {\ frac {ar} {2}} = {\ frac {pr} {2}}}$ ${\ displaystyle \ quad = {\ tfrac {1} {4}} na^{2} \ kiságy ({\ tfrac {\ pi} {n}})}$ ${\ displaystyle \ quad = nr^{2} \ tan ({\ tfrac {\ pi} {n}})}$ ${\ displaystyle \ quad = {\ tfrac {1} {4n}} p^{2} \ kiságy ({\ tfrac {\ pi} {n}})}$ ${\ displaystyle \ quad = {\ tfrac {1} {2}} nR^{2} \ sin ({\ tfrac {2 \ pi} {n}}) \, \!}$	${\ displaystyle p = na \}$( Kerülete ) beírt kör sugara körülírt sugara ${\ displaystyle r = {\ tfrac {a} {2}} \ kiságy ({\ tfrac {\ pi} {n}}),}$ ${\ displaystyle {\ tfrac {a} {2}} = r \ tan ({\ tfrac {\ pi} {n}}) = R \ sin ({\ tfrac {\ pi} {n}})}$ ${\ displaystyle r:}$ ${\ displaystyle R:}$
Kör	${\ displaystyle A = \ pi r^{2} = {\ frac {\ pi d^{2}} {4}}}$ ( átmérő ) ${\ displaystyle d = 2r:}$
Körkörös szektor	${\ displaystyle A = {\ frac {\ theta} {2}} r^{2} = {\ frac {L \ cdot r} {2}} \, \!}$
Ellipszis	${\ displaystyle A = \ pi ab \, \!}$
Integrál	${\ displaystyle A = \ int _ {a}^{b} f (x) \ mathrm {d} x, \ f (x) \ geq 0}$
	Felszíni terület
Szféra	${\ displaystyle A = 4 \ pi r^{2} = \ pi d^{2}}$
Kocka alakú	${\ displaystyle A = 2 (ab+ac+bc)}$
henger (alul és felül)	${\ displaystyle A = 2 \ pi r (r+h)}$
Kúp (alul is)	${\ displaystyle A = \ pi r (r+{\ sqrt {r^{2}+h^{2}}})}$
Torus	${\ displaystyle A = 4 \ pi ^{2} \ cdot R \ cdot r}$
A forradalom felszíne	${\ displaystyle A = 2 \ pi \ int _ {a}^{b} \! f (x) {\ sqrt {1+ \ left [f '(x) \ right]^{2}}} \ mathrm { d} x}$ (forgatás az x tengely körül)

A fenti számítások megmutatják, hogyan lehet megtalálni sok közös alakzat területét .

A szabálytalan (és így tetszőleges) sokszögek területeit a " Felmérő képlet " (cipőfűző képlet) segítségével lehet kiszámítani .

A terület viszonya a kerülethez

Az izoperimetrikus egyenlőtlenség kimondja, hogy az L hosszúságú zárt görbére (tehát a környező terület L kerülete ) és az általa bezárt régió A területére ,

${\ displaystyle 4 \ pi A \ leq L^{2},}$

és az egyenlőség akkor és csak akkor érvényes, ha a görbe kör . Így egy körnek van egy adott kerületével rendelkező zárt alakja közül a legnagyobb területe.

A másik végletben egy adott L kerületű alak tetszőlegesen kis területtel rendelkezhet, amint azt egy rombusz szemlélteti, amely tetszőlegesen "felborul", úgy, hogy két szöge tetszőlegesen 0 ° közelben van, a másik kettő pedig tetszőlegesen közel 180 ° -ra.

Egy kör esetében a terület és a kerület aránya (a kör kerületének kifejezése) egyenlő az r sugár felével . Ez látható a πr ² területképletből és a 2 πr kerületképletből .

Egy szabályos sokszög területe a kerületének fele az apotéma (ahol az apotéma a középpont és a legközelebbi pont közötti távolság bármelyik oldalon).

Fraktálok

Ha egy sokszög élhosszát megduplázzuk, akkor négyszer megszorozzuk a területét, ami kettővel (az új és a régi oldalhossz aránya) a kettő hatványára emelve (a tér mérete, amelyben a sokszög található). De ha a két dimenzióban megrajzolt fraktál egydimenziós hosszait mind megduplázzuk, akkor a fraktál térbeli tartalma két olyan erővel skálázódik, amely nem feltétlenül egész szám. Ezt az erőt a fraktál fraktáldimenziójának nevezik .

Területfelezők

Végtelen számú egyenes van, amely kettészeli a háromszög területét. Közülük három a háromszög mediánja (amely összeköti az oldalak középpontját a szemközti csúcsokkal), és ezek egyidejűek a háromszög középpontjában ; Valójában ők az egyetlen területfelező, amely átmegy a centroidon. Bármely sor egy háromszög osztja mind a háromszög területe és kerülete fele átmegy a háromszög incenter (a központ az beírt ). Ezekből egy, kettő vagy három van egy adott háromszögre.

A paralelogramma felezőpontján átmenő bármely vonal kettészeli a területet.

Egy kör vagy más ellipszis minden területfelezője átmegy a középponton, a középponton keresztül húzódó akkordok pedig felezik a területet. Egy kör esetén ezek a kör átmérői.

Optimalizálás

Tekintettel a huzal kontúrjára, a legkisebb átfogó felület ("töltés") minimális felület . Ismerős példák a szappanbuborékok .

A kérdés az betöltési területet a Riemann kör nyitva marad.

A kör a legnagyobb területtel rendelkezik az azonos kerületű kétdimenziós objektumok közül.

Egy ciklikus sokszögnek (egy körbe írtnak) van a legnagyobb területe minden sokszögből, adott számú oldala azonos hosszúságú.

A háromszögek izoperimetrikus egyenlőtlenségének egyik változata szerint az adott kerületűek közül a legnagyobb területű háromszög egyenlő oldalú .

Az adott körbe írtak közül a legnagyobb területű háromszög egyenlő oldalú; és az adott kör köré írt körök közül a legkisebb területű háromszög egyenlő oldalú.

Az incircle és az egyenlő oldalú háromszög területének aránya nagyobb, mint bármely nem egyenlő oldalú háromszögé. ${\ displaystyle {\ frac {\ pi} {3 {\ sqrt {3}}}}}$

A terület és az egyenlő oldalú háromszög kerülete négyzetének aránya nagyobb, mint bármely más háromszögé. ${\ displaystyle {\ frac {1} {12 {\ sqrt {3}}}},}$

Lásd még

• Brahmagupta négyszög , ciklikus négyszög egész oldalakkal, egész átlókkal és egész területtel.
• Equiareal térkép
• Gémes háromszög , háromszög egész oldalakkal és egész területtel.
• Háromszög egyenlőtlenségek listája
• Egy hetedik terület háromszög , egy belső háromszög a referencia háromszög területének hetedével.

• Routh tétele , az egyhetedik területi háromszög általánosítása.

• Nagyságrendek - A területek méret szerinti listája.
• Az ötszög képletének levezetése
• Planimeter , eszköz kis területek mérésére, pl. Térképeken.
• Egy domború négyszög területe
• Robbins ötszög , egy ciklikus ötszög, amelynek oldalhossza és területe mind racionális számok.

Hivatkozások

Külső linkek